Частная производная от потенциальной энергии по какой-либо внешней силе равна перемещению по направлению этой силы.
Пусть к упругой конструкции приложено n сосредоточенных сил P i.
P1 P2 P i P n
Изгибающий момент в произвольном сечении выразим на основе принципа суперпозиции:
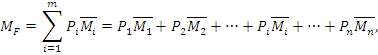
где 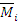 – изгибающий момент от действия единичной силы
– изгибающий момент от действия единичной силы 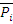 =1.
=1.
Найдем частную производную от изгибающего момента по силе P i:
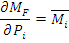
Потенциальная энергия деформации равна:
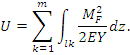
Возьмем частную производную от энергии по силе P i:
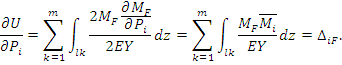
 2015-04-30
2015-04-30 496
496








