Мы установили статические (1) и геометрические (2 а) зависимости. Для того, чтобы согласовать их между собой, воспользуемся законом Гука (какова деформация, такова сила,à какова сила, такова деформация).

Где элементы 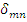 матрицы
матрицы 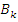 есть абсолютные деформации по направлению m обобщенной силы, вызыванные действием единичной обобщенной силы в n направлении.
есть абсолютные деформации по направлению m обобщенной силы, вызыванные действием единичной обобщенной силы в n направлении.
Рассмотрим схему стержня, эквивалентную заданной:
| Ni |
Qi lk F2=Qi
F3=Mi
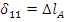
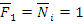
При действии продольной силы 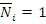 стержень удлиняется на
стержень удлиняется на 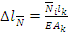 , т.к.
, т.к.
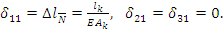
При действии поперечной силы 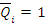 стержень изгибается, образуя прогиб и угол поворота.
стержень изгибается, образуя прогиб и угол поворота.
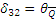
|
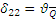
|
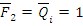

При действии изгибающего момента 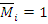 стержень так же изгибается, образуя прогибы и угол поворота.
стержень так же изгибается, образуя прогибы и угол поворота.

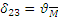
|
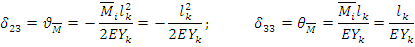
Матрица Bk принимает вид:
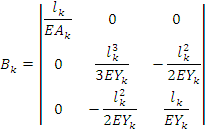
Закон Гука можно записать в прямой форме (какова деформация, такова сила):
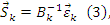 где обратная матрица
где обратная матрица 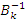 имеет вид:
имеет вид:

Подставим зависимость (3) и (2 а) в (1) (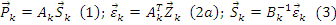 ) и получим:
) и получим:
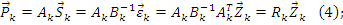
Где 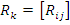 - матрица жесткости для k стержня, имеющего узлы i, j. В развернутом виде матрицу жесткости стержня для случая α=0 (
- матрица жесткости для k стержня, имеющего узлы i, j. В развернутом виде матрицу жесткости стержня для случая α=0 (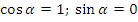 ) можно записать так:
) можно записать так:
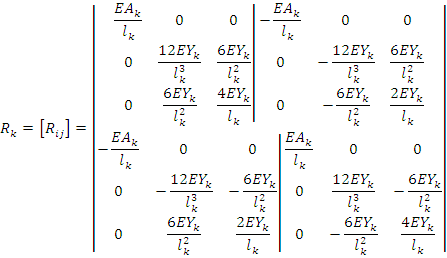
Анализ отдельно взятого стержня закончен. Можно переходить к синтезу, т.е. к рассмотрению всей системы в целом. Исходные данные следующие:
1. Координаты узлов системы – геометрическая информация;
2. Жесткости поперечных сечений стержней – физическая информация;
3. Стержневая связь между узлами – топологическая информация;
4. Внешние нагрузки – статическая информация.
Требуется определить:
1. Усилия 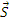 во всех стрежнях;
во всех стрежнях;
2. Перемещения 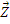 всех узлов.
всех узлов.
Обозначим: 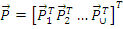 – вектор узловых нагрузок системы;
– вектор узловых нагрузок системы;
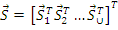 - вектор внутренних усилий системы;
- вектор внутренних усилий системы;
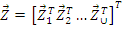 - вектор узловых перемещений системы;
- вектор узловых перемещений системы;
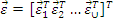 - вектор абсолютных деформаций системы;
- вектор абсолютных деформаций системы;
А – матрица равновесия системы;
В – матрица податливости системы;
R – матрица жесткости системы.
Для поставленной задачи имеем:
1. Уравнения равновесия
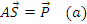
2. Геометрические уравнения

3. Физические зависимости закона Гука
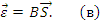
Так как в число неизвестных входят только усилия 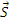 и перемещения
и перемещения 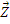 , то исключим из трех видов уравнений вектор деформации
, то исключим из трех видов уравнений вектор деформации 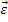 . Подставим (а), (б), (в):
. Подставим (а), (б), (в):

Объединим уравнения (а) и (г) в одну систему:
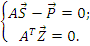 (д)
(д)
Матрица А имеет 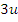 строк и 3 S столбцов (u – число узлов, S – число стержней). Матрица
строк и 3 S столбцов (u – число узлов, S – число стержней). Матрица 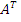 имеет 3 S строк и
имеет 3 S строк и 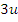 столбцов.
столбцов.
Первое векторное уравнение содержит 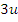 алгебраических уравнений с 3 S неизвестными, а второе векторное уравнение - 3 S алгебраических уравнений с
алгебраических уравнений с 3 S неизвестными, а второе векторное уравнение - 3 S алгебраических уравнений с 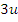 неизвестными. Всего уравнений
неизвестными. Всего уравнений 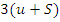 ; число неизвестных так же равно
; число неизвестных так же равно 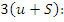 каждый узел имеет 3 перемещения, а каждый стержень 3 усилия.
каждый узел имеет 3 перемещения, а каждый стержень 3 усилия.
Выразим из второго векторного уравнения вектор усилий 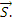
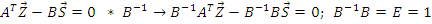
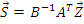
Подставим в первое векторное уравнение:

где 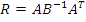 - матрица жесткости системы.
- матрица жесткости системы.
Решая уравнение с 3 u неизвестными 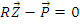 находим перемещения всех узлов системы:
находим перемещения всех узлов системы:
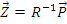
Затем вычисляем усилия во всех стержнях системы:
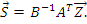
 2015-04-30
2015-04-30 443
443








