Как плоские, пространственные системы подразделяют на системы сходящихся или произвольно расположенных сил. Многоугольник, построенный на сходящихся силах системы, оказывается пространственным, что делает невозможным применение графического и графоаналитического методов решения. Аналитический метод решения аналогичен изложенному для плоских систем с той лишь разницей, что силы проецируются на три (а не на две) взаимно перпендикулярные оси, а моменты сил определяются относительно этих осей (а не точек). Необходимо помнить, что момент силы относительно оси равен нулю в том случае, когда сила и ось лежат в одной плоскости (т.е. линия действия силы или параллельна оси, или пересекает ее).
Вопросы для самоконтроля
1. Напишите уравнения равновесия для пространственной системы сходящихся сил.
2. Что такое момент силы относительно оси? В каких случаях момент силы относительно оси равен нулю?
3. Напишите уравнения равновесия для произвольной пространственной системы сил.
В результате изучения темы студент должен:
иметь представление о параллелепипеде сил, приведении пространственной системы сил к главному вектору и к главному моменту;
знать определение моментов относительно оси, условия равновесия пространственной системы сил.
Тема 1.6 Центр тяжести тела
Тема относительно проста для усвоения, однако крайне важна при изучении курса сопротивления материалов. Главное внимание здесь необходимо обратить на решение задач как с плоскими и геометрическими фигурами, так и со стандартными прокатными профилями.
Вопросы для самоконтроля
1. Что такое центр параллельных сил?
2. Как найти координаты центра параллельных сил?
3. Что такое центр тяжести тела?
4. Как найти центр тяжести прямоугольника, треугольника, круга?
5. Как найти координаты центра тяжести плоского составного сечения?
6. Центр тяжести

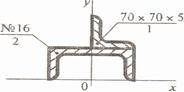
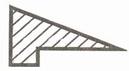
1 В каком случае для определения центра тяжести достаточно определить одну координату расчетным путем?
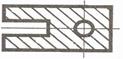
2 Как учитывается площадь отверстия в фигуре 4 в формуле для определения центра тяжести фигуры?
В результате изучения темы студент должен:
иметь представление о центре параллельных сил и его свойствах;
знать формулы для определения координат центра тяжести плоских фигур;
уметь определять координаты центра тяжести плоских фигур простых геометрических фигур и стандартных прокатных профилей.
 2015-04-30
2015-04-30 2098
2098
