Двигателей с лопаточными пазами ротора

Фигурный стержень литой обмотки ротора будем рассматривать как двойную клетку ротора, причем к пусковой клетке отнесем верхнюю (прямоугольную или полуовальную – в зависимости от формы фигурного паза) часть стержня, а к рабочей клетке – его нижнюю часть.

Без большой погрешности можно принять 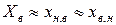, так как эти сопротивле­ния обусловлены проводимостью верхней части паза и

.

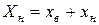При принятом допущении система уравнений может быть записана следующим образом:

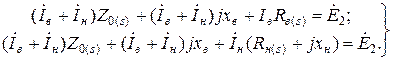(11.2.1)

Системе уравнений (11.2.1) соответствует схема замещения, при­веденная на рис. 11.2.1, которая может служить исходной для опреде­ления параметров двухклеточного ротора. Практические формулы для расчета и 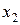роторов с общими и раздельными замыкающими кольцами несколько различаются.

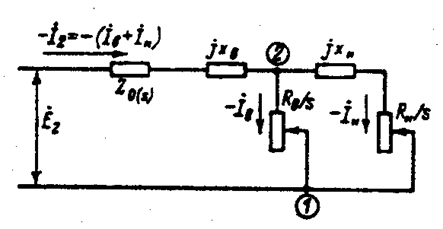
Рис. 11.2.1. Преобразованная схема замещения фазы короткозамкнутого ротора с лопаточными пазами

Рассмотрим вначале метод расчета 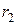и 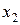роторов с общими за­мыкающими кольцами. Для таких роторов коэффициенты при неизвестных токах в уравнениях (11.2.1) обозначают следующие сопротивления: 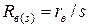— активное сопротивление стержня верхней клети; 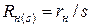— активное сопротивление стержня нижней клетки; 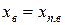— индуктивное сопротивление рассеяния стержня верхней клетки; 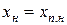— индуктивное сопротивление пазового рассеяния стержня нижней клетки.

,

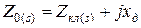где 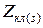–– сопротивление участков замыкающих колец между двумя, соседними пазами, приведенное к току ротора;

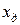— индуктивное сопротивление дифференциального рассеяния обмотки ротора.

Эквивалентное сопротивление разветвленной цепи этой схемы между толками 1—2

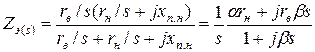, (11.2.2)

где

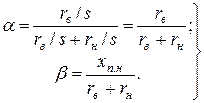(11.2.3)

Представим 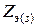в виде суммы активного 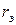и индуктивного 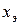сопротивлений:

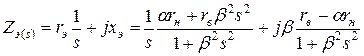
и упростим выражение для 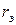и :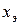

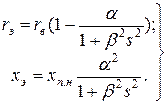(11.2.4)

Сопротивления 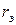и 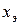зависят от скольжения, так как изменение соотношения активных и индуктивных сопротивлений стержней вызванное изменением частоты тока в роторе, изменяет соотношение токов в стержнях рабочей и пусковой клеток.

При скольжениях 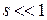, соответствующих холостому ходу и номинальному режиму двигателей, из (11.2.4) получим

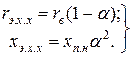(11.2.5)

Коэффициенты изменения эквивалентных сопротивлени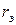й и 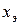в зависимости от скольжения

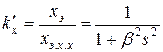; (11.2.6)

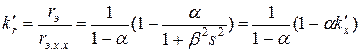. (11.2.7)

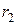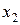На основании полученных соотношений запишем основные расчетные формулы для определения и двухклеточных роторов с общими замыкающими кольцами (двухклеточные роторы с литыми обмотками и роторы с фигурны­ми пазами).

При 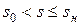активное сопротивление фазы ротора, Ом,

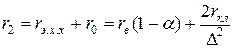, (11.2.8)

где α –– по (11.2.3), причем

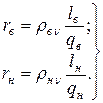(11.2.9)

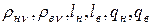— удельные сопротивления при расчетной темпера­туре, длины и площади поперечных сечений стержней верхней и ниж­ней клеток; при литых обмотках с общими замыкающими кольцами в 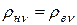и 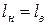; Δ — см. (6.2).

Индуктивное сопротивление фазы ротора, Ом,

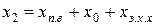, (11.2.10)

где

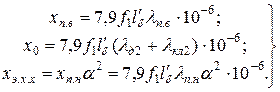(11.2.11)

С учетом (11.2.11)

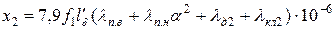, (11.2.12)

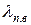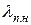где и — коэффициенты магнитных проводимостей потоков пазового рассеяния соответственно верхней и нижней клеток, которые определяются в зависимости от конфигурации пазов верхней и нижней клеток по формулам табл. 11.2.1;

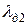— коэффициент магнит­ной проводимости дифференциального рассеяния ротора, который определяется по (8.31);

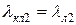— коэффициент магнитной проводимости участков замыкающего кольца, приведенный к току ротора, который определяется по (8.29) или по (8.30).

Таблица 11.2.1. Расчетные формулы для определения коэффициента магнитной проводимости пазового рассеяния роторов с фигурными пазами

Рисунок	Расчетные формулы
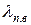
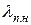
11.2.2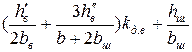

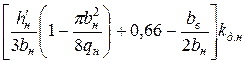
Примечание: 1. При закрытых пазах ротора коэффициент магнитной проводимости 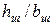рассчитывать в соответствии с указаниями, приведенными § 8 (см. рис.8.7).

2. При расчете параметров холостого хода и номинального режима принимать .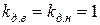

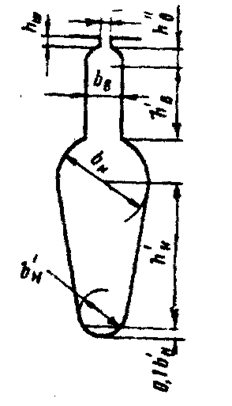
Рис. 11.2.2. К расчету коэффициентов магнитной проводимости пазового рассеяния двухклеточных короткозамкнутых роторов с фигурными пазами

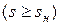
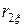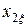Для пусковых режимов и роторов с общими замыкающими кольцами рассчитывают по следующим формулам.

Активное сопротивление фазы ротора, Ом,

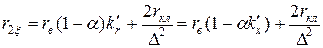. (11.2.13)

Индуктивное сопротивление фазы ротора, Ом,

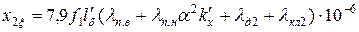. (11.2.14)

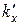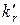В этих формулах и рассчитывают по (11.2.6) и (11.2.7), в ко­торых α и β определяют по (11.2.3), а 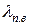и 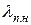для пазов, показан­ных на рис. 11.2.2, — по формулам табл. 11.2.1.

Предполагают, что плотность тока в пределах сечения каждого из стержней постоянна. Пр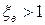и и 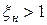можно несколько повы­сить точность расчета, учитывая влияние эффекта вытеснения тока на сопротивления каждого из стержней. Для этого по формулам приведенным в § 11.1, последовательно рассчитывают для верхнего стержня 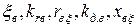и для нижнего стержня 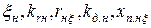после чего определяют

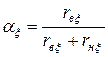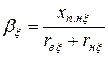; . (11.2.15)

подставляя эти величины вместо α и β последующие формулы, находят 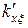и 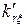и по (11.2.13) и (11.2.14) рассчитывают 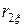и 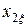с учетом влияния эффекта вытеснения тока на сопротивление каждого из стерж­ней обмотки при принятых значе­ниях s. Обычно 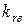и 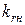близки к единице, и уточнения расчета, свя­занного с влиянием эффекта вы­теснения тока на каждый из стержней, не требуется.

Для уточнения расчета пускового момента и тока следует учесть также влияние насыщения от полей рассеяния на проводи­мость паза верхней клетки. Расчет проводят аналогично изложенно­му в § 11.1.

При расчете сопротивлений роторов с раздельными замыкаю­щими кольцами (двухклеточные роторы с обмоткой из вставных стержней) аналогично принятому ранее допущению (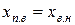) при­нимают, что индуктивное сопро­тивление участков замыкающего кольца верхней клетки приблизи­тельно равно сопротивлению взаимоиндуктивности участков колец верхней и нижней клеток. Такое допущение позволяет испо­льзовать ту же схему замещения (см. рис. 11.2.1), но с несколько изме­ненными значениями ее параметров. В схеме замещения ротора с раздельными кольцами:

сумма активных сопротивлений стержня и участков замыкающих колец верхней клетки

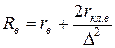; (11.2.16)

сумма активных сопротивлений стержня и участков замыкающих колец нижней клетки

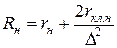; (11.2.17)

сумма индуктивных сопротивлений пазового рассеяния и участков замыкающих колец верхней клетки

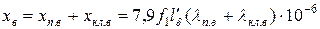; (11.2.18)

сумма индуктивных сопротивлений пазового рассеяния и учаков замыкающих колец нижней клетки

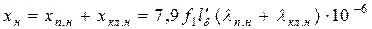; (11.2.19)

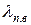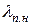В этих выражениях и — коэффициенты магнитной проводимости пазового рассеяния соответственно верхней и нижней клеток (рассчитываются в зависимости от конфигурации пазов ц данным табл. 11.3);

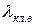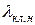, — коэффициенты магнитной проводимости участков замыкающих колец [рассчитываются по (8.29) или (8.30)].

Общее сопротивление для обеих параллельных ветвей схемы замещения

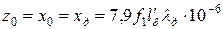. (11.2.20)

где 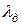— коэффициент магнитной проводимости дифференциального рассеяния, рассчитываемый по (8.31).

Сопротивления 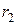и 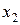роторов с раздельными замыкающими кольцами для холостого хода и номинального режима работы, Ом,

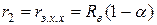; (11.2.21)

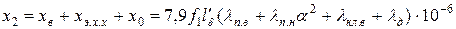; (11.2.22)

где

.

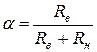Сопротивления 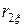и 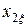для пусковых режимов работы, Ом,

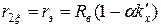; (11.2.23)

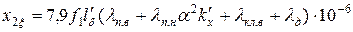; (11.2.24)

где 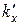определяется по (11.2.6) при

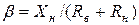. (11.2.25)

Эффект вытеснения тока в каждом из стержней и влияние насыщения полями рассеяния на параметры ротора учитывают так же, как и для роторов с общими замыкающими кольцами.

Приведенный метод расчета параметров двухклеточных роторов и роторов с фигурными пазами, как и другие аналогичные ему методы, учитывающие индуктивную связь только между полными токами каждого из стержней, являются приближенными, однако они находят применение в расчетной практике благодаря своей простоте.