Производная и дифференциал сложной функции

Производная сложной функции.

Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда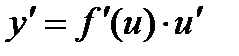

Доказательство.

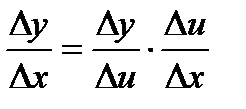
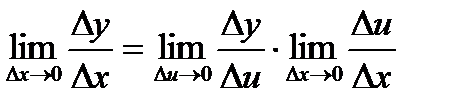
(с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)

Тогда 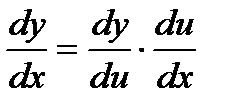. Теорема доказана.