2015-04-20
678
Пусть на отрезке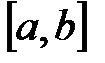 
задана функция 
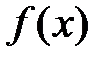и определена система функций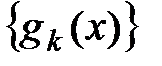 
.
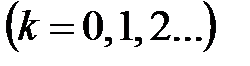Обобщенным многочленом (полиномом) порядка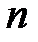 
(степени 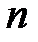) относительно системы функций 
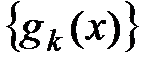называют функцию вида
,
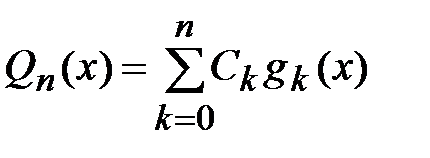где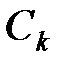 
- некоторые постоянные.
Обобщенный многочлен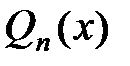 
называется многочленом наилучшего среднеквадратичного приближения функции 
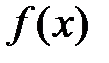, если расстояние от функции до многочлена по среднеквадратичной норме (среднеквадратичное отклонение) наименьшее, т. е.
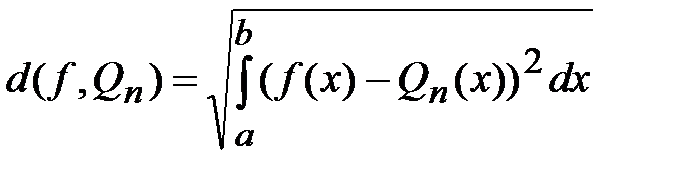- наименьшее. (3.1)
Задачу нахождения такого многочлена называют задачей об интегральном среднеквадратичном приближении (аппроксимации) функции 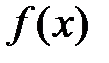на отрезке 
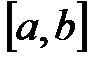обобщенным многочленом. Задача сводится к нахождению коэффициентов 
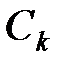из условия о наименьшем 
:
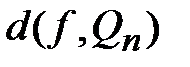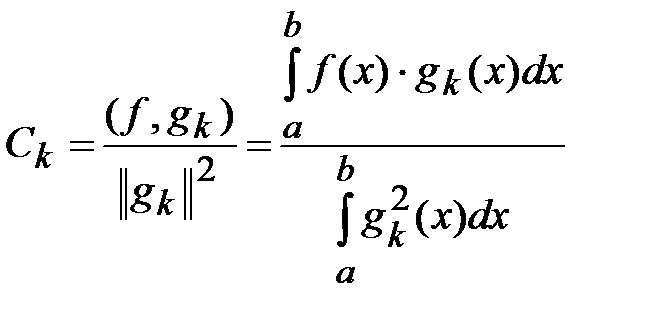, k=0, 1, 2,…, n. (3.2)
Скалярное произведение функци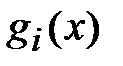й 
и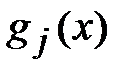 
на отрезке 
:
.
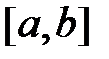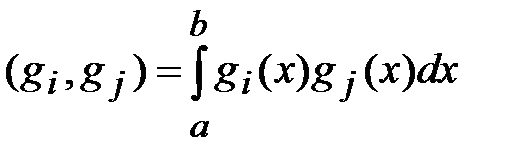Норма функции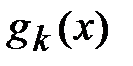 
на отрезке :
.
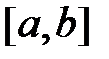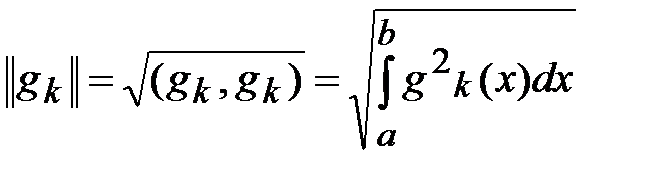Квадрат наименьшего среднеквадратичного отклонения определяется соотношением
,
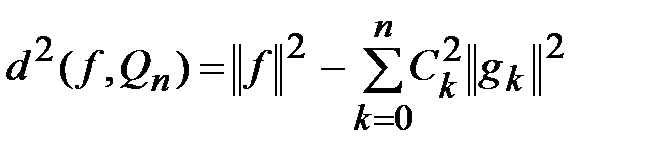где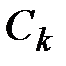 
- коэффициенты Фурье, определяемые по формуле (3.2).
Пусть задана система тригонометрических функций
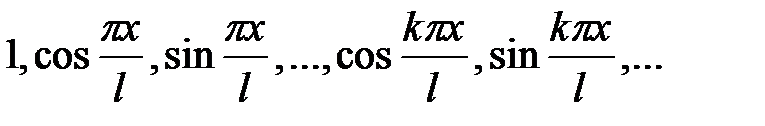
на отрезке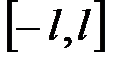 
. Для функции 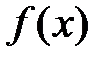, интегрируемой с квадратом на отрезке 
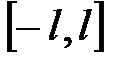, тригонометрическим многочленом наилучшего среднеквадратичного приближения является тригонометрический многочлен
,
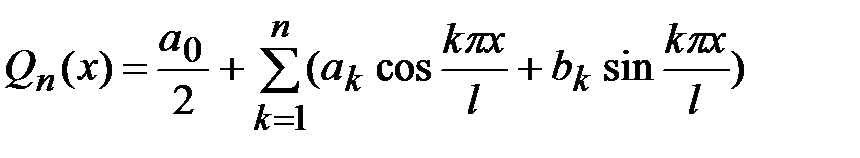где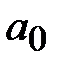 
, 
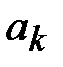и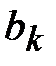 
- коэффициенты Фурье по тригонометрической системе функций, определяемые по формулам
,
,
.
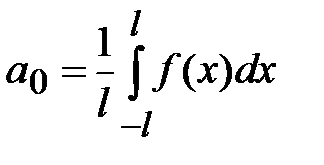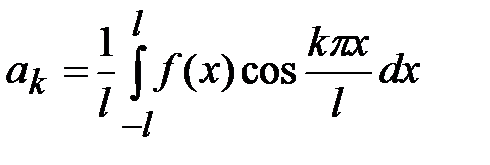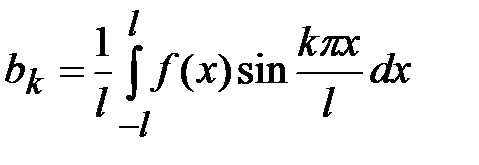Среднеквадратичное отклонение аппроксимирующего многочлена от функции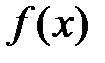 
в данном случае выражается равенством
.
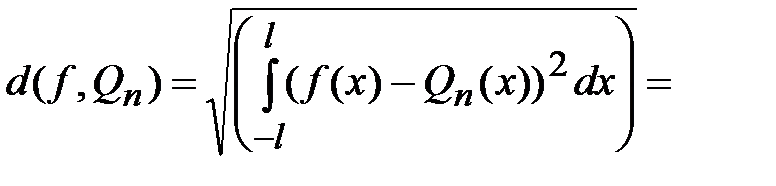
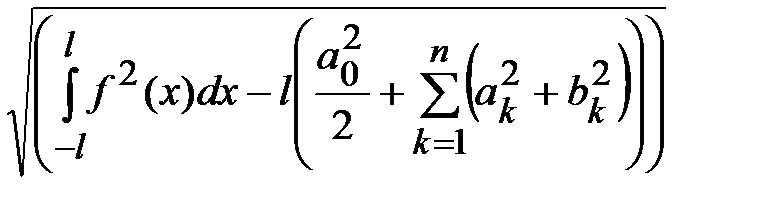Среднеквадратичное отклонение, отнесенное к норме аппроксимируемой функции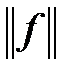 
, характеризует точность приближения и обозначается
.
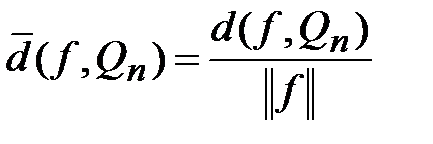Аппроксимация тригонометрическими многочленами предназначена для работы с аналитически заданными функциями.
