Линейная алгебра

ЗАДАЧА 1

Вычислить определитель.

1.1. 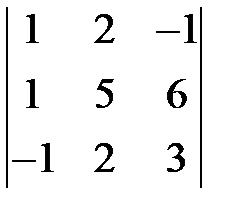. 1.2. 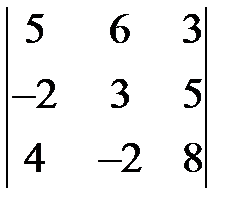. 1.3. 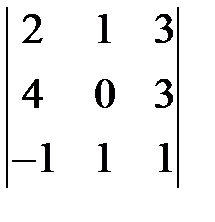. 1.4. .

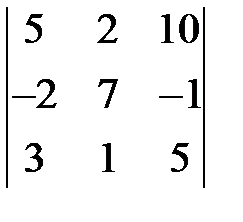1.5. 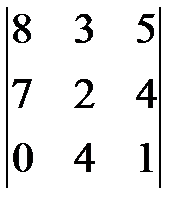. 1.6. 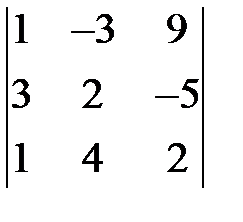. 1.7. 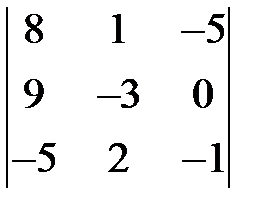. 1.8. 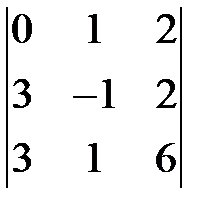. 1.9. 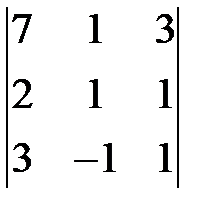. 1.10. .

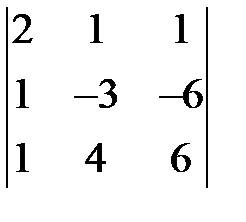ЗАДАЧА 2

Найти матрицу Х из матричного уравнения (решать, используя обратную матрицу).

2.1. 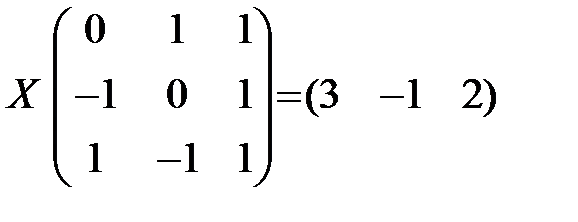. 2.2. .

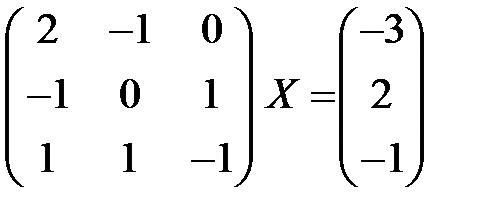2.3. 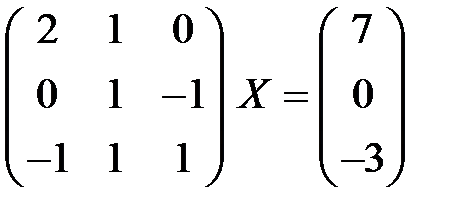. 2.4. .

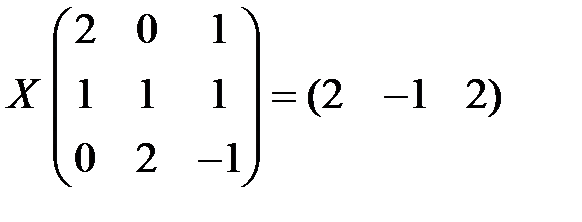2.5. 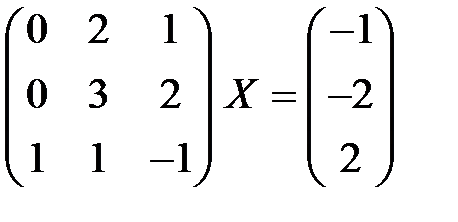. 2.6. .

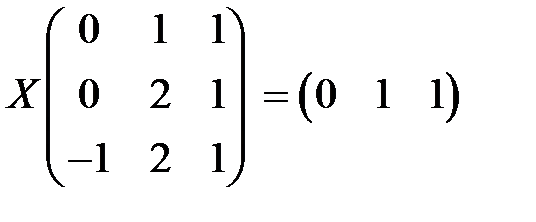2.7. 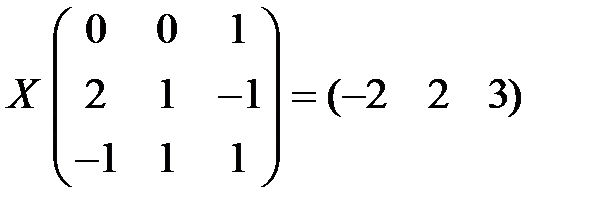. 2.8. .

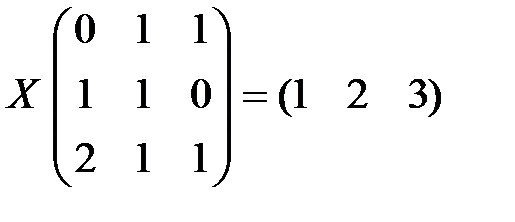2.9. 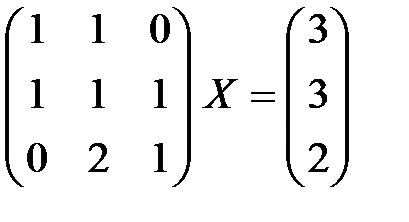. 2.10. .

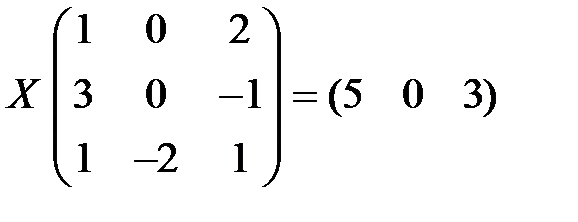ЗАДАЧА 3

Решить систему уравнений методом Гаусса.

3.1. 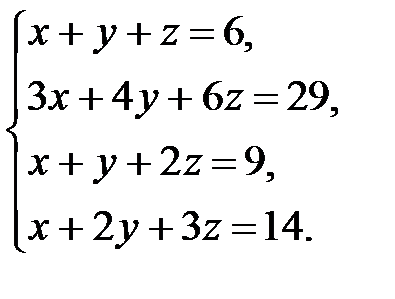. 3.2. 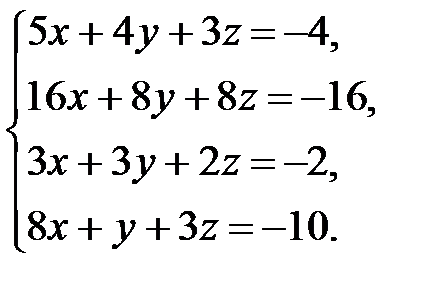. 3.3. .

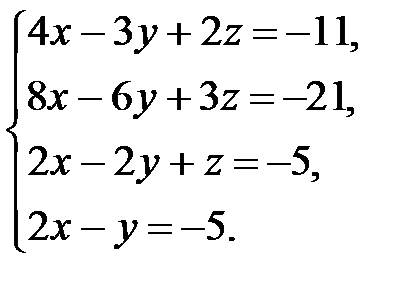3.4. 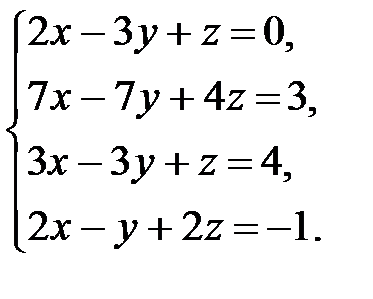. 3.5. 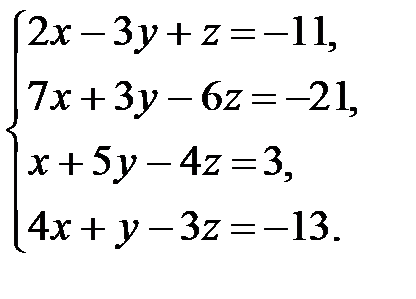. 3.6. .

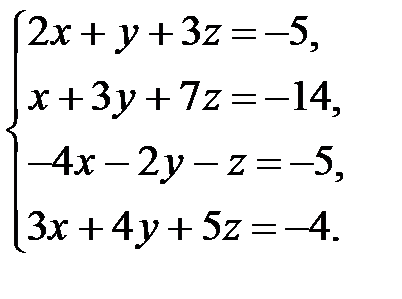3.7. 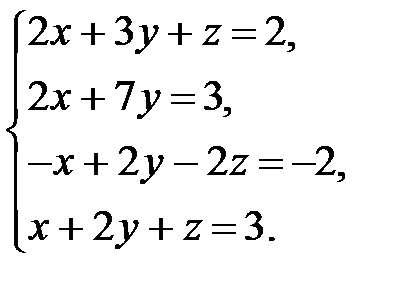. 3.8. 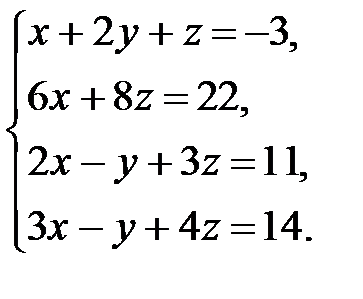. 3.9. .

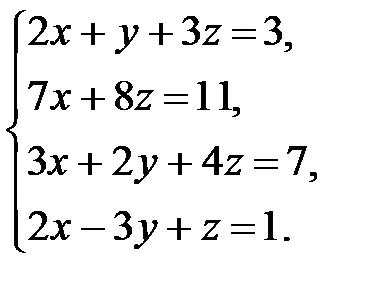3.10. .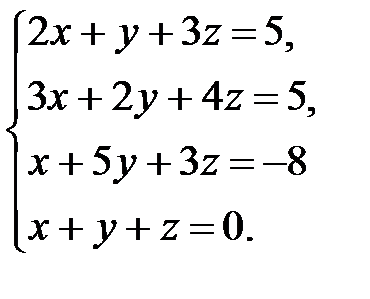

Векторная алгебра

ЗАДАЧА 4

Найти площадь и длины диагоналей параллелограмма, построенного на векторах .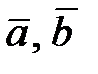

4.1. .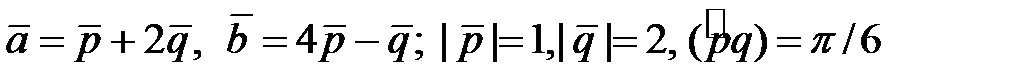

4.2. .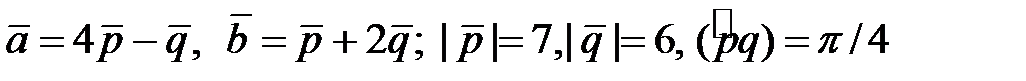

4.3. .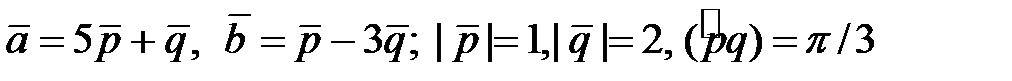

4.4. .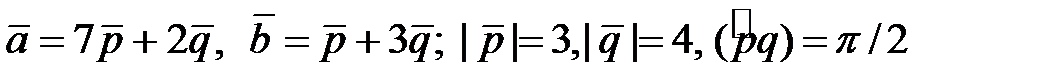

4.5. .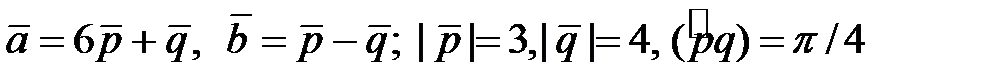

4.6. .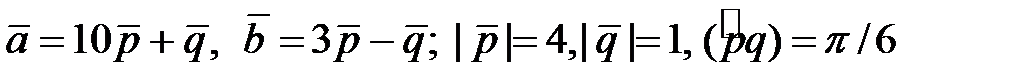

4.7. .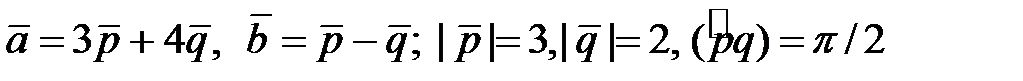

4.8. .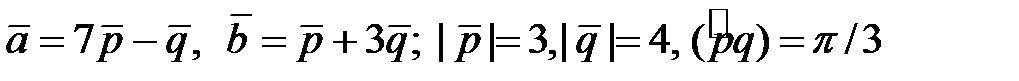

4.9. .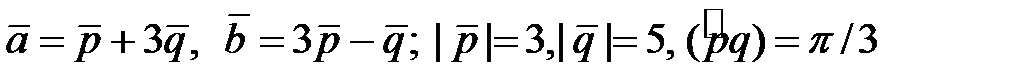

4.10. .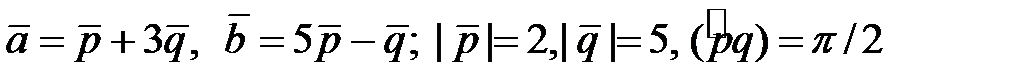

ЗАДАЧА 5

Даны вершины треугольника А, В, С. Найти косинус угла ВАС, проекцию стороны АВ на сторону АС и площадь треугольника АВС.

5.1. A (1;–2;3); B (0;–1;2); C (4;0;4). 5.2. A (0;–3;6); B (–12;–3;–3); C (–9; –3;–6).

5.3. A (3;3;–1); B (5;5;–2); C (4;1; 1). 5.4. A (–1;2;–3); B (3;4;–6); C (1;1;–1).

5.5. A (–4;–2;0); B (–1;–2;4); C (3;–2;1). 5.6. A (5;3;–1); B (5;2;0); C (6;4;–1).

5.7. A (–3;–7;–5); B (0;–1;–2); C (-5;-6;-6). 5.8. A (3;3;–1); B (1;–5;2); C (4;4;1).

5.9. A (2;1;–1); B (6;–1;–4); C (4;2;1). 5.10. A (3;–6;9); B (0;–3;6); C (5;-3;7).

ЗАДАЧА 6

Вычислить объем тетраэдра с вершинами в точках A, B, C, D.

6.1. A (14;4;5), B (–5;–3;2), C (–2;–6;–3), D (–2;2;–1).

6.2. A (1;2;0), B (3;0;–3), C (5;2;6), D (8;4;–9).

6.3. A (2;–1;2), B (1;2;–1), C (3;2;1), D (–4;2;5).

6.4. A (2;–1;2), B (1;2;–1), C (3;2;1), D (–4;2;5).

6.5. A (1;1;2), B (–1;1;3), C (2;–2;4), D (–1;0;–2).

6.6. A (2;3;1), B (4;1;–2), C (6;3;7), D (7;5;–3).

6.7. A (1;5;–7), B (–3;6;3), C (–2;7;3), D (–4;8;–12).

6.8. A (–3;4;–7), B (1;5;–4), C (–5;–2;0), D (2;5;4).

6.9. A (–1;2;–3), B (4;–1;0), C (2;1;–2), D (3;4;5).

6.10. A (4;–1;3), B (–2;1;0), C (0;–5;1), D (3;2;–6).

Аналитическая геометрия