К простейшим задачам аналитической геометрии относятся задачи вычисления расстояния между двумя точками, деления отрезка в данном отношении и нахождения площади треугольника.
1. Расстояние между двумя точками. Расстояние между двумя точками А и В равно длине вектора 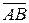 :
:
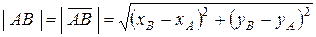 , (3.1)
, (3.1)
где 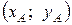 – координаты точки А,
– координаты точки А, 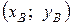 – координаты точки В.
– координаты точки В.
2. 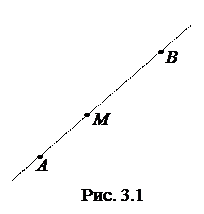 Деление отрезка в данном отношении.
Деление отрезка в данном отношении.
2 Отношением, в котором точка М делит отрезок АВ (рис. 3.1) называется число 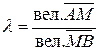 .
.
Если точка М находится между точками А и В, то величины направленных отрезков 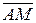 и
и 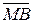 будут одного и того же знака независимо от выбора направления на прямой АВ. В этом случае число l будет больше нуля. Если же точка М находится за пределами отрезка АВ, то число l меньше нуля.
будут одного и того же знака независимо от выбора направления на прямой АВ. В этом случае число l будет больше нуля. Если же точка М находится за пределами отрезка АВ, то число l меньше нуля.
g Координаты точки М, делящей отрезок АВ в отношении 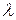 можно найти по формулам:
можно найти по формулам:
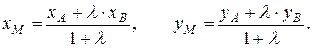 (3.2)
(3.2)
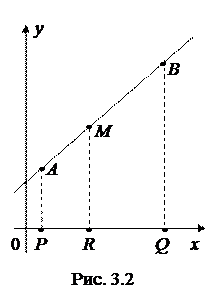 4 Спроектируем точки А, В, и М на ось Ox (рис. 3.2). Очевидно, что точка R (проекция точки М) делит отрезок PQ в отношении
4 Спроектируем точки А, В, и М на ось Ox (рис. 3.2). Очевидно, что точка R (проекция точки М) делит отрезок PQ в отношении 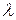 . Следовательно,
. Следовательно, 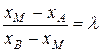 . Из последнего равенства выразим xM:
. Из последнего равенства выразим xM: 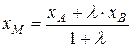 . Аналогично, проектируя точки А, В, и М на ось Oy, получаем, что
. Аналогично, проектируя точки А, В, и М на ось Oy, получаем, что
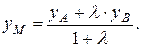 3
3
В частности, когда точка М делит отрезок АВ пополам, то 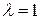 и формулы (3.2) примут вид:
и формулы (3.2) примут вид:
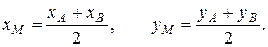 (3.3)
(3.3)
3. Вычисление площади треугольника.
g Площадь треугольника АВС, вершины которого имеют координаты
(xA; yA), (xB; yB), (xC; yC) равна
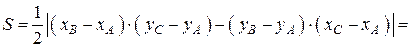
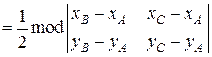 . (3.4)
. (3.4)
4 Если рассматривать треугольник ABC в трехмерном пространстве, то его вершины будут иметь координаты: A (xA; yA; 0), B (xB; yB; 0), C (xC; yC; 0). Площадь треугольника можно найти по формуле (2.8): 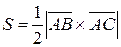 , где
, где 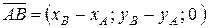 ,
, 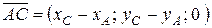 .
.
Сначала найдем векторное произведение векторов 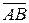 и
и 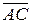 по формуле (2.12):
по формуле (2.12):
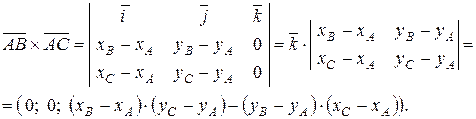
Таким образом,
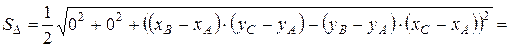
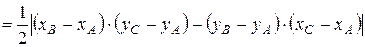 .3
.3
Задача 3.1. Дан треугольник A (2; 7), B (–5; 7), C (5; 3). Найти:
1) длины сторон треугольника ABC; 2) площадь треугольника; 3) основание биссектрисы AF угла А.
Решение. 1) Длины сторон найдем по формуле (3.1):
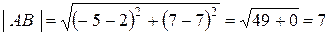 (ед),
(ед),
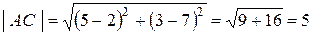 (ед),
(ед),
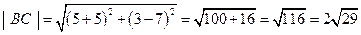 (ед).
(ед).
2) Площадь треугольника вычислим по формуле (3.4):
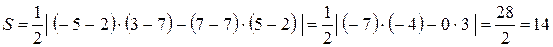 (ед 2).
(ед 2).
3) Основание биссектрисы AF (точку F) найдем, используя то, что точка F делит противоположную сторону BC треугольника на части, пропорциональные прилежащим сторонам:
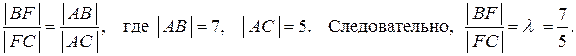
Для нахождения координат точки F используем формулы деления отрезка в данном отношении (3.2):
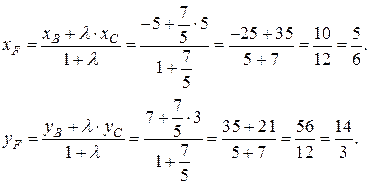
 2015-04-01
2015-04-01 7899
7899








