Числовые множества, операции над множествами

Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые.

Сравнение множеств

Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент B:

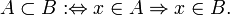
В этом случае A называется подмножеством B, B — надмножеством A. Есл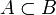и и 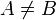, то A называется собственным подмножеством B. Заметим, что 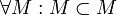. По определению .

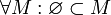Два множества называются равными, если они являются подмножествами друг друга:

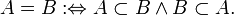
Иногда для того, чтобы подчеркнуть, что множества могут быть равны, используется запись:

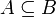
[править]Операции над множествами

[править] Бинарные операции

Ниже перечислены основные операции над множествами:

§ пересечение:

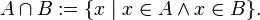
§ объединение:

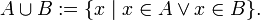
Если множества A и B не пересекаются: 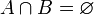, то их объединение обозначают также: .

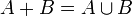§ разность (дополнение):

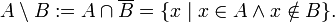
§ симметрическая разность:

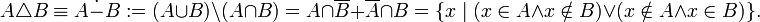
§ Декартово или прямое произведение:

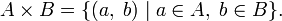
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.

[править] Унарные операции

§ Абсолютное дополнение:

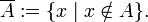
Операция дополнения подразумевает некоторый универсум (универсальное множество U, которое содержит A):

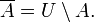
Относительным же дополнением называется А\В (см.выше):

§ Мощность множества:

| A |

Результатом является кардинальное число (для конечных множеств — натуральное).

§ Множество всех подмножеств (булеан):

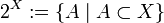
Обозначение происходит из того, что 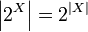в случае конечных множеств.

[править]Приоритет выполнения операций

Сначала выполняются операции дополнения, затем пересечения, объединения и разности, которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками.