Учитывая высокую крутизну кривой Парето она может быть аппроксимирована. Пусть координата n по оси абсцисс будет соответствовать 1 (у нас n =6, что соответствует 1). Обозначим ось абсцисс F, а ось ординат V.
Тогда для уравнения кривой Парето получим:
V=4×F, 0£ F£ 0.2, (9)
V=1/4×F+3/4, 0.2£ F£ 1.0 (10)
Аппроксимированная кривая Парето представлена на рис.3.
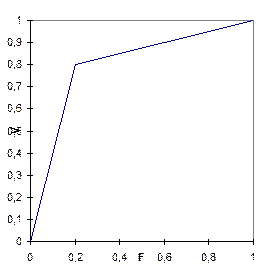 |
Рис. 3. Аппроксимированная кривая Парето
Кроме этого метода известен также другой метод, который получил название «Метод окружности». По показателю «жескости» он занимает промежуточное положение между методом парных сравнений и методом Парето. Существо этого метода заключается в том, что на диаграмме Парето строят часть окружности единичного радиуса с центром в точке с координатами (0; 1).
Уравнение окружности имеет вид
(F-F0)2 + (V-V0)2 = R2 (11)
Для F0 = 1, V0 = 0 и R=1 получим
(F-1)2+V2=1 (12)
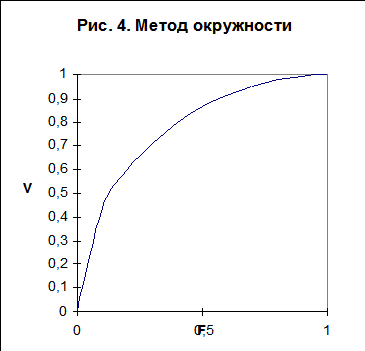
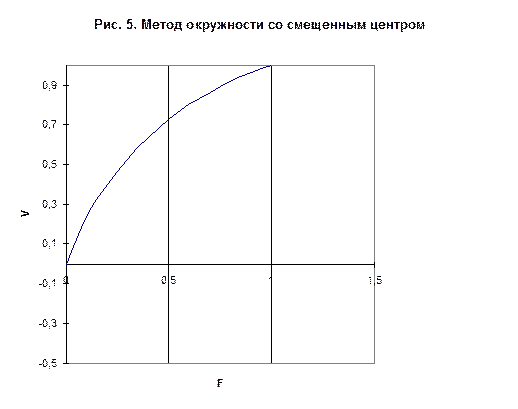
На рисунке 4 представлена кривая Лоуренса, построенная для весовых коэффициентов, определенных по методу окружности, а на рисунке 5 - кривая Лоуренса, построенная для весовых коэффициентов, определенных по методу окружности со смещенным центром. Центр окружности лежит на диагонали 4-й четверти.
Распределение весовых коэффициентов по методу окружности со смещенным центром, соответственно, «мягче», чем аналогичное распределение по методу окружности.
 |
 |
Неравномерное распределение весовых коэффициентов для различных факторов наблюдается всегда и везде. Нет правильных или неправильных распределений. Есть только объективно существующие распределения и ваши субъективные.
Список литературы
1. SPSS BASE 8.0. Руководство по применению SPSS. – М.: СПСС РУСЬ. 1998.
2. Айвазян С.А., Мхитарян В.С. Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т.1: Теория вероятностей и прикладная статистика. – М.: ЮНИТИ-ДАНА, 2001. – 656 с.
3. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы: Учебник. – М.: Финансы и статистика, 2000. – 352 с.: ил.
4. Дюк В., Самойленко А. Data Mining: Учебный курс + CD. – СПб: Питер, 2001. – 368 с.: ил.
5. Шурыгин А.М. Прикладная стохастика: робастность, оценивание, прогноз. – М.: Финансы и статистика, 2000. – 224 с.: ил.
 2015-04-30
2015-04-30 908
908








