Лекция 2.
Пример 1. Решить начальную задачу для ОДУ первого порядка 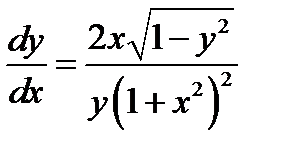 ,
, 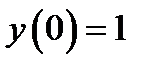 .
.
Решение. Определяем тип уравнения. Правая часть ОДУ состоит из сомножителей, каждый из которых зависит от одной переменной. Уравнение с разделяющимися переменными. Разделяем переменные. 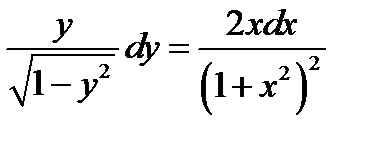 . Интегрируя обе части, получаем
. Интегрируя обе части, получаем
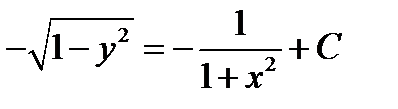 . Подставляя в общее решение значения
. Подставляя в общее решение значения 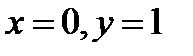 ,получаем
,получаем 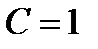 .
.
Находим явное выражение для 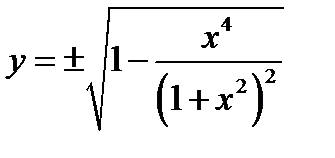 . Учитывая начальное условие
. Учитывая начальное условие 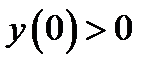 получаем, что решение начальной задачи имеет вид
получаем, что решение начальной задачи имеет вид 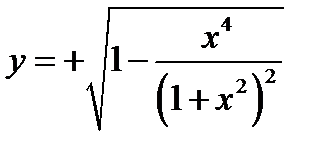 .
.
Пример 2. Решить начальную задачу 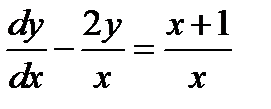 ,
, 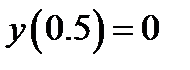 .
.
Решение. Определяем тип ОДУ. Данное уравнение линейное.
1 шаг. Находим интегрирующий множитель 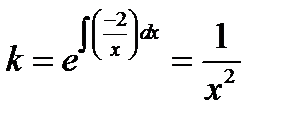 .
.
2 шаг. Умножая обе части уравнения на полученный на первом шаге множитель, имеем
 . Отсюда
. Отсюда 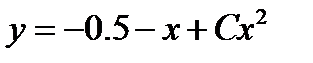 . Подставляя начальные данные
. Подставляя начальные данные 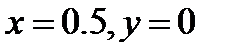
получаем 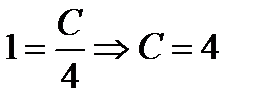 . Решение начальной задачи имеет вид
. Решение начальной задачи имеет вид 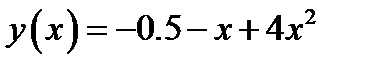 .
.
 2015-04-30
2015-04-30 240
240







