33. Если F(x) – одна из первообразных функции f(x),то 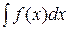 = …
= …
34. Производная от интеграла 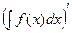 равна …
равна …
35. Дифференциал от интеграла 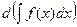 равен …
равен …
36. Интеграл 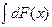 равен …
равен …
37. Если 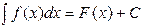 , то
, то 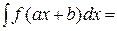 …
…
38. Если функция 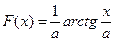 первообразная функции
первообразная функции 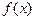 , то функция f(x) равна
, то функция f(x) равна
39. Если 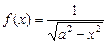 , то ее первообразная
, то ее первообразная 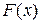 равна …
равна …
40. Чему равен интеграл 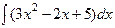 …
…
41. Чему равен интеграл 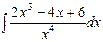 …
…
42. 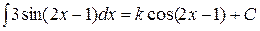 . Тогда k = …
. Тогда k = …
43. 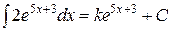 . Тогда k = …
. Тогда k = …
44. Найдите интегралы: а) 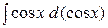 ; б)
; б) 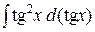 ; в)
; в) 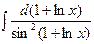 ;
;
г) 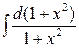 ; д)
; д) 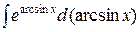 .
.
45. Какую из подстановок целесообразно использовать для замены переменной в интеграле: а) 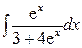 ; б)
; б) 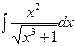 ; в)
; в) 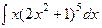 ; г)
; г) 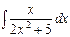 ;
;
д) 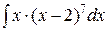 .
.
46. Какое из выражений целесообразно принять за U при интегрировании по частям интеграла: а) 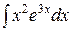 ; б)
; б) 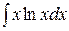 ; в)
; в) 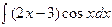 ; г)
; г) 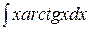 .
.
47. Какое из выражений целесообразно принять за dV при интегрировании по частям интеграла: а) 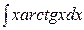 ; б)
; б) 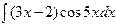 ; в)
; в) 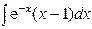 ; г)
; г) 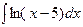 .
.
48. Если F(x) является первообразной функции f(x), то справедлива формула Ньютона-Лейбница …
49. Вычислить определенные интегралы: а) 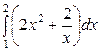 ; б)
; б) 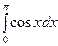 ;
;
в) 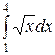 ; г)
; г) 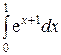 .
.
50. Вычислить определенные интегралы методом замены переменной:
а) 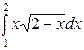 ; б)
; б) 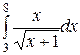 ; в)
; в) 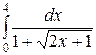
51. Вычислить определенные интегралы интегрированием по частям:
а) 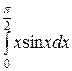 ; б)
; б) 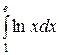 ; в)
; в) 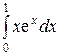 .
.
52. Найти площадь фигуры, ограниченной линиями:
а) у = х3, у = 0, х = 1;
б) у = х2, у = 1, х = 0.
1. Вычислить определитель 2-го порядка
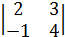 .
.
РЕШЕНИЕ:
Вычисление определителя 2-го порядка проводится по формуле:
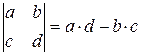 , поэтому для нашей задачи имеем:
, поэтому для нашей задачи имеем:
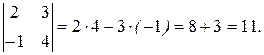
2. Вычислить определитель 3-го порядка, пользуясь правилом треугольника
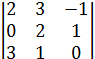 .
.
РЕШЕНИЕ
Вычисление определителя 3-го порядка по правилу треугольника проводится по схеме
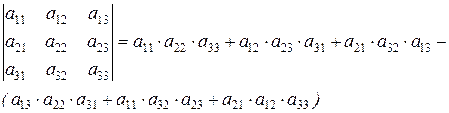
3. Вычислить определитель 3-го порядка методом разложения по элементам второй строки
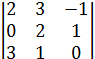 .
.
РЕШЕНИЕ
Вычисление определителя 3-го порядка методом разложения по элементам второй строки проводится по следующей формуле:

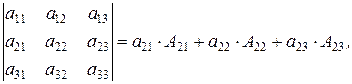
где 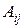 — алгебраические дополнения элементов
— алгебраические дополнения элементов 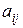 в данном определителе:
в данном определителе:
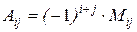 , а
, а 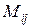 — миноры, соответствующие элементам
— миноры, соответствующие элементам 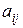 определителя, которые являются определителями второго порядка, получаемые из данного определителя путем вычеркивания строки i и столбца j.
определителя, которые являются определителями второго порядка, получаемые из данного определителя путем вычеркивания строки i и столбца j.
Следовательно, мы имеем:
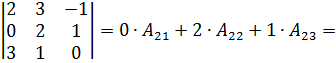
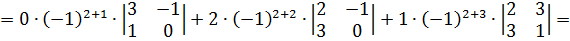
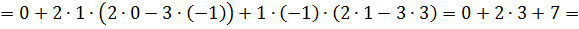
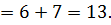
4. Найти произведение двух матриц A и B, если
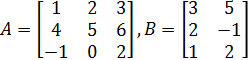 .
.
РЕШЕНИЕ
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Рассмотрим на примере:
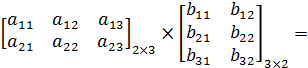
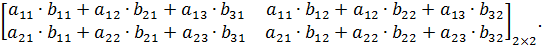
В нашем случае имеем:
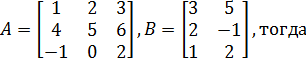
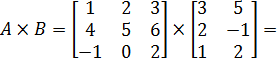
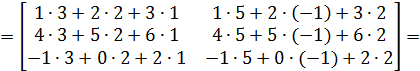
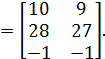
5. Найти матрицу 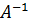 , обратную для матрицы A, где
, обратную для матрицы A, где
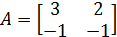 .
.
РЕШЕНИЕ
Обратная матрица находится по следующей формуле:
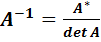 , где
, где 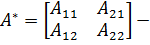 союзная матрица к матрице
союзная матрица к матрице 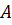 , а
, а 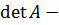 определитель, составленный из элементов данной матрицы. Подставляя, получаем:
определитель, составленный из элементов данной матрицы. Подставляя, получаем: 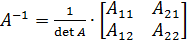 . В нашем случае:
. В нашем случае:
1. Находим определитель данной матрицы:
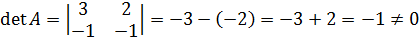 , следовательно обратная матрица существует.
, следовательно обратная матрица существует.
2. Находим союзную матрицу к матрице 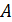 , т.е.
, т.е. 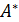 . Для этого найдем алгебраические дополнения элементов
. Для этого найдем алгебраические дополнения элементов 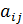 в данной матрице (см. пример № 3):
в данной матрице (см. пример № 3):
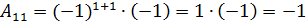 ;
; 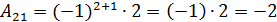 ;
;
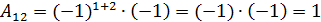 ;
; 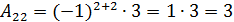 .
.
Получаем:
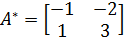
3. Подставляем полученные результаты в формулу и находим обратную матрицу 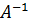 :
: 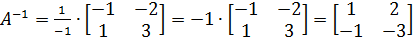 .
.
6. Найти длину вектора 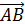 , если А (1;2;3), В (4;6;3).
, если А (1;2;3), В (4;6;3).
РЕШЕНИЕ
Для нахождения длины заданного вектора вначале найдем его координаты по формуле 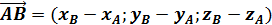 , где
, где 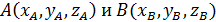 . Затем по формуле
. Затем по формуле 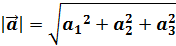 , где
, где 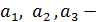 координаты вектора
координаты вектора 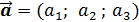 , найдем его длину. В нашем случае получаем:
, найдем его длину. В нашем случае получаем:
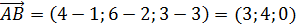 , тогда, подставляя координаты в формулу нахождения длины вектора, получаем:
, тогда, подставляя координаты в формулу нахождения длины вектора, получаем:
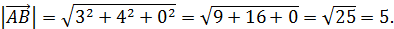
7. Вычислить скалярное произведение векторов 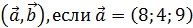
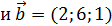 .
.
РЕШЕНИЕ
Для вычисления скалярного произведения векторов пользуются следующей формулой:
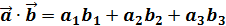 ,где
,где 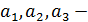 координаты вектора
координаты вектора 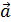 , а
, а 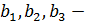 координаты вектора
координаты вектора 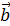 . В нашем случае получаем:
. В нашем случае получаем:
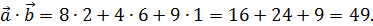
8. Найти 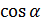 между векторами
между векторами 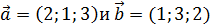 .
.
РЕШЕНИЕ
Для того, чтобы найти косинус угла между векторами воспользуемся следующей формулой:
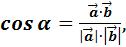 где в числителе стоит скалярное произведение данных векторов (см. пример №7), а в знаменателе произведение их длин (см. пример №6). Найдем вначале скалярное произведение данных векторов:
где в числителе стоит скалярное произведение данных векторов (см. пример №7), а в знаменателе произведение их длин (см. пример №6). Найдем вначале скалярное произведение данных векторов:
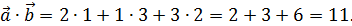 Теперь найдем их длины:
Теперь найдем их длины:
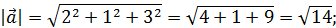
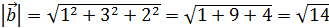 .
.
Подставляем найденные значения в формулу:
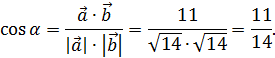
9. Написать общее уравнение прямой на плоскости, проходящей через две точки А (2;-1) и В (-3;2).
РЕШЕНИЕ
Общее уравнение прямой на плоскости, проходящей через две точки, имеет вид:
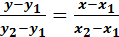 , где
, где 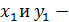 координаты одной из точек, а
координаты одной из точек, а 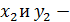 другой.
другой.
В нашем случае это уравнение примет вид:
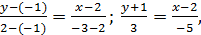 отсюда, воспользовавшись свойством пропорции, получим:
отсюда, воспользовавшись свойством пропорции, получим: 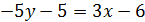 , выразим из этого равенства
, выразим из этого равенства 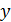 :
:
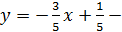 уравнение прямой на плоскости, проходящей через две данные точки.
уравнение прямой на плоскости, проходящей через две данные точки.
10. Найти точку пересечения двух прямых на плоскости, заданных общими уравнениями:
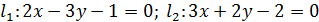 .
.
РЕШЕНИЕ
Для нахождения точки пересечения двух прямых, нужно составить систему из их общих уравнений и решить ее относительно 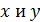 .
.
Полученные значения и будут координатами точки пересечения данных прямых. В нашем случае получается:
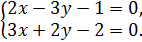
Для решения данной системы умножим первое уравнение на 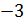 , а второе на
, а второе на 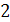 :
:
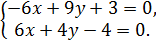
Теперь сложим почленно первое и второе уравнения:
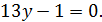
Получили линейное уравнение, найдем из него 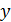 :
:
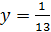 .
.
Чтобы найти 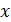 подставим
подставим 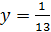 в любое из исходных уравнений, ну, например, во второе:
в любое из исходных уравнений, ну, например, во второе:
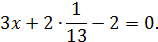
Приведем подобные члены и выразим 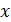 :
:
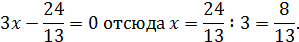
Тогда точка пересечения данных прямых имеет следующие координаты: 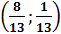 .
.
11. Написать уравнение прямой, проходящей через точку А (2;-1) параллельно вектору 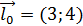 .
.
РЕШЕНИЕ
Уравнение прямой, проходящей через данную точку 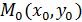 , параллельно заданному вектору
, параллельно заданному вектору 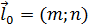 записывается в виде:
записывается в виде:
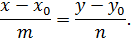
В нашем случае, получаем:
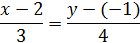
Отсюда получаем:
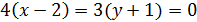 ;
;
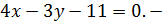 искомое уравнение
искомое уравнение
12. Написать уравнение прямой, проходящей через точку А (2;-1) перпендикулярно вектору 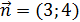 .
.
РЕШЕНИЕ
Уравнение прямой, проходящей через данную точку 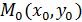 , перпендикулярно заданному вектору
, перпендикулярно заданному вектору 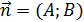 , записывается в виде:
, записывается в виде:
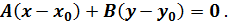
В нашем случае получаем следующее уравнение:
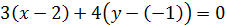 , раскроем скобки и приведем подобные члены
, раскроем скобки и приведем подобные члены
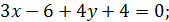
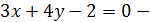 искомое уравнение.
искомое уравнение.
13. Вычислить пределы:
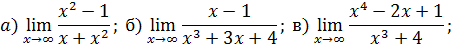
РЕШЕНИЕ
a) 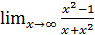 . При решении данного предела возникает неопределенность вида
. При решении данного предела возникает неопределенность вида  . Чтобы избавиться от неопределенности разделим числитель и знаменатель дроби на
. Чтобы избавиться от неопределенности разделим числитель и знаменатель дроби на 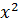 :
:
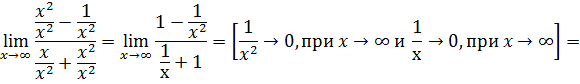
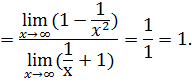
б) 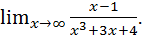 При решении данного предела возникает неопределенность вида
При решении данного предела возникает неопределенность вида  . Чтобы избавиться от неопределенности разделим числитель и знаменатель дроби на
. Чтобы избавиться от неопределенности разделим числитель и знаменатель дроби на 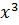 :
:
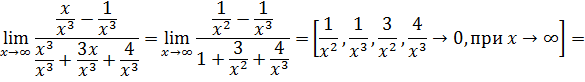
в) 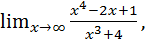 при решении данного предела возникает неопределенность вида
при решении данного предела возникает неопределенность вида  . Чтобы избавиться от неопределенности, разделим числитель и знаменатель дроби на
. Чтобы избавиться от неопределенности, разделим числитель и знаменатель дроби на 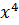 :
:
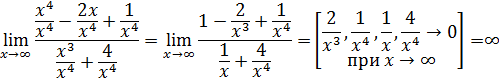
Так как предел числителя равен 1, а в знаменателе стоит бесконечно малая при 
14. Вычислить пределы:
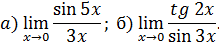
РЕШЕНИЕ
a) 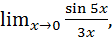 при решении данного предела возникает неопределенность вида
при решении данного предела возникает неопределенность вида  .
.
Чтобы избавиться от неопределенности, можно поступить следующим образом:
1 способ. Обозначим 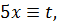 тогда при
тогда при 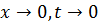 . Подставляя, получаем:
. Подставляя, получаем:
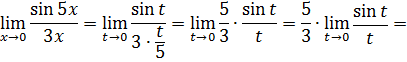
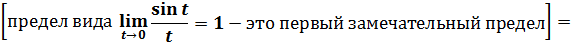
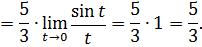
2 способ. Заметим, что при 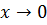 функция
функция 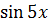 является бесконечно малой (б.м.), следовательно, ее можно заменить эквивалентной, т.е. получаем, что
является бесконечно малой (б.м.), следовательно, ее можно заменить эквивалентной, т.е. получаем, что 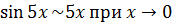 . Подставляя в наш предел, получаем:
. Подставляя в наш предел, получаем:
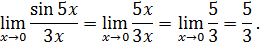
б) 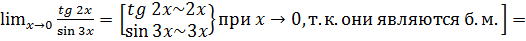
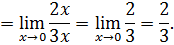
15. Найти производные следующих функций:
а) 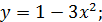
б) 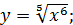
в) 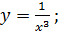
г) 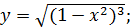
д) 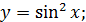
е) 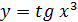 .
.
РЕШЕНИЕ
а) Для нахождения данной производной воспользуемся формулой отыскания производной степенной функции 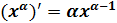 и производной разности
и производной разности 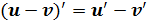 . В нашем случае имеем:
. В нашем случае имеем:
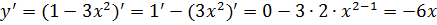 ;
;
б) Воспользуемся свойством корня n – ой степени: 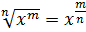 . Тогда получаем:
. Тогда получаем: 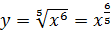 . Для нахождения производной воспользуемся формулой
. Для нахождения производной воспользуемся формулой 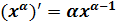 .
.
Значит 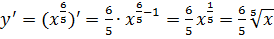 .
.
в) Воспользуемся формулой для нахождения производной представленной в пункте а), учитывая, что: 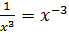 .
.
Тогда получаем:
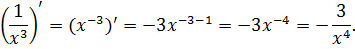
г) 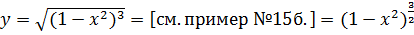 . Обратим внимание, что это сложная функция.
. Обратим внимание, что это сложная функция.
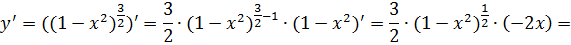
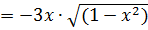 .
.
д) Здесь нам понадобиться формула нахождения производной тригонометрической функции 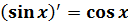 и степенной функции (см. пример №15а).
и степенной функции (см. пример №15а).
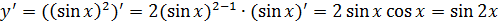 .
.
е) Здесь нам понадобиться формула нахождения производной тригонометрической функции 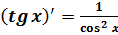 и степенной функции (см. пример №15а).
и степенной функции (см. пример №15а).
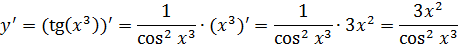
16. Используя правило Лопиталя, найти пределы:
а) 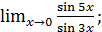
б) 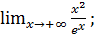
в) 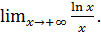
РЕШЕНИЕ
Согласно правилу Лопиталя:
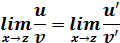
Для неопределенностей вида 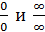 .
.
Тогда в нашем случае:
а) 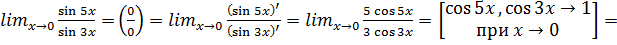
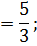
б) 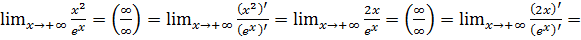
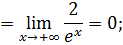
в) 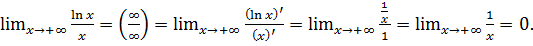
17. Найти интервалы возрастания и убывания следующих функций:
а) 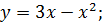
б) 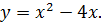
РЕШЕНИЕ
Для нахождения интервалов возрастания и убывания функции используется следующий алгоритм:
1. Находим область определения функции 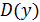 ;
;
2. Находим производную заданной функции;
3. Приравниваем производную к нулю и находим корни получившегося уравнения;
4. При помощи найденных корней разбиваем нашу область определения на интервалы и находим знак производной на каждом из них;
5. Если производная на интервале знакопостоянства меньше ноля то функция на этом интервале убывает, и наоборот – если производная больше 0, то функция на этом интервале возрастает.
Для наших примеров:
а) 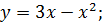
Следуя алгоритму получаем:
1. 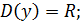
2. 
3. 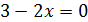
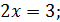
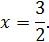

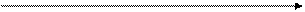 + 1,5 --
+ 1,5 --
4. Таким образом, получаем, что наша функция возрастает на интервале 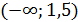 , а убывает на интервале
, а убывает на интервале 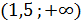 .
.
б) 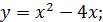
Следуя алгоритму получаем:
1. 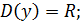
2. 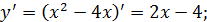
3. 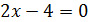
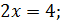
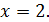
4. 
 2 +
2 +
Таким образом, получаем, что наша функция возрастает на итервале
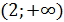 , а убывает на интервале
, а убывает на интервале 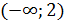 .
.
18. Исследовать на экстремум следующие функции:
а) 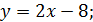
б) 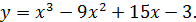
РЕШЕНИЕ
Схема исследования на экстремум функции одной переменной:
1. Найти область определения;
2. Найти 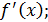
3. Найти критические точки, т.е. значения аргумента, при которых производная 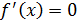 или не существует;
или не существует;
4. Критическими точками разбить область определения на интервалы знакопостоянства и установить знак производной в каждом интервале;
5. Если при переходе через критическую точку производная меняет знак с (+) на (-), то в этой критической точке максимум, если 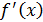 меняет знак с (-) на (+), то в этой критической точке минимум. Если
меняет знак с (-) на (+), то в этой критической точке минимум. Если 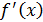 не изменяет знак, то данная критическая точка не является экстремальной.
не изменяет знак, то данная критическая точка не является экстремальной.
Для наших примеров:
а) 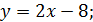
Следуя алгоритму получаем:
1. 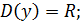
2. 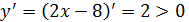 при любом
при любом 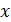 . Дальнейшее исследование нецелесообразно, т.к. функция является монотонно возрастающей на всей области определения R.
. Дальнейшее исследование нецелесообразно, т.к. функция является монотонно возрастающей на всей области определения R.
б) 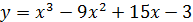
Следуя алгоритму получаем:
1. 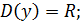
2. 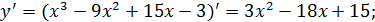
3. 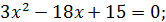
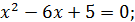
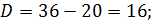
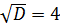 ;
;
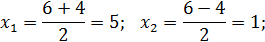
4. 

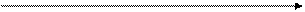 + 1
+ 1 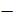 5 +
5 +
5. В критической точке 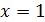 находится максимум функции, а в критической точке
находится максимум функции, а в критической точке 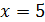 – минимум функции.
– минимум функции.
19. Вычислить неопределенные интегралы:
а) 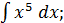
б) 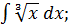
в) 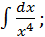
г) 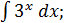
д) 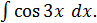
РЕШЕНИЕ
а) Это табличный интеграл и находится он по следующей формуле:
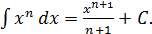 Тогда для нашего случая имеем:
Тогда для нашего случая имеем:
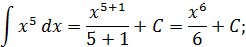
б) 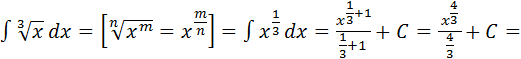
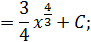
в) 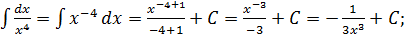
г) 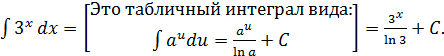
д) 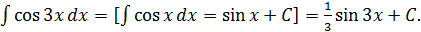
20. Применяя формулу Ньютона – Лейбница, вычислить определенные интегралы:
а) 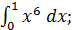
б) 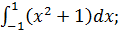
в) 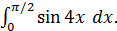
РЕШЕНИЕ
Формула Ньютона – Лейбница имеет вид:
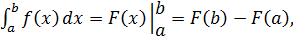 где
где 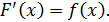
В нашем случае получаем:
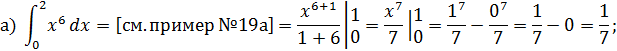
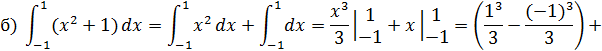
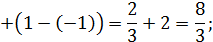
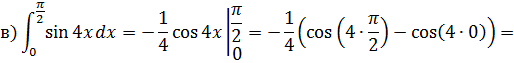
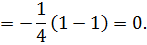
21. Найти частные производные первого порядка от следующих функций:
а) 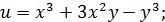
б) 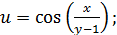
в) 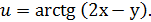
РЕШЕНИЕ
Частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции 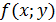 находятся по формулам и правилам вычисления производных функции одной переменной (при этом другая переменная, соответственно
находятся по формулам и правилам вычисления производных функции одной переменной (при этом другая переменная, соответственно 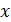 или
или 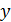 считается постоянной величиной).
считается постоянной величиной).
В нашем случае имеем:
а) 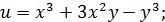
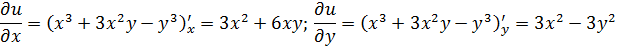
б) 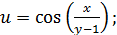
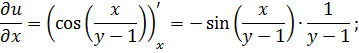
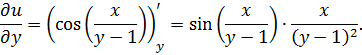
в) 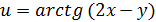 ;
;
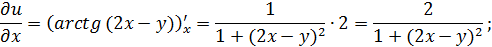
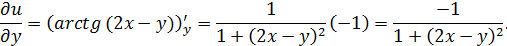
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ:
1. Гурский, Е. Н. Основы линейной алгебры и аналитической геометрии. 2-е изд. доп. – Минск: Выш. шк., 1982. – 272 с.
2. Жевняк, Р. М. Высшая математика. / Р. М. Жевняк, А. А. Карпук. – Минск: Выш.шк., 1984 – 1988. – Ч.1 – 384 с.
3. Пискунов, Н. С. Дифференциальное и интегральное исчисление. – М.: Наука, 1985 – Т. 1 – 456 с.
4. Письменный Д.Т. Конспект лекций по высшей математике: полный курс / – 9-е изд. – М.: Айрис-пресс, 2009.
4. Сборник индивидуальных заданий по высшей математике / под ред. А. П. Рябушко. – Минск: Выш. шк., 1990 – 1991. – Ч.1 – 270 с.
 2015-04-20
2015-04-20 880
880







