Решение. 1. Раскрываем статическую неопределимость

1. Раскрываем статическую неопределимость.

Определяем степень статической неопределимости.

.

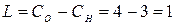Выбираем основную систему (ОС)

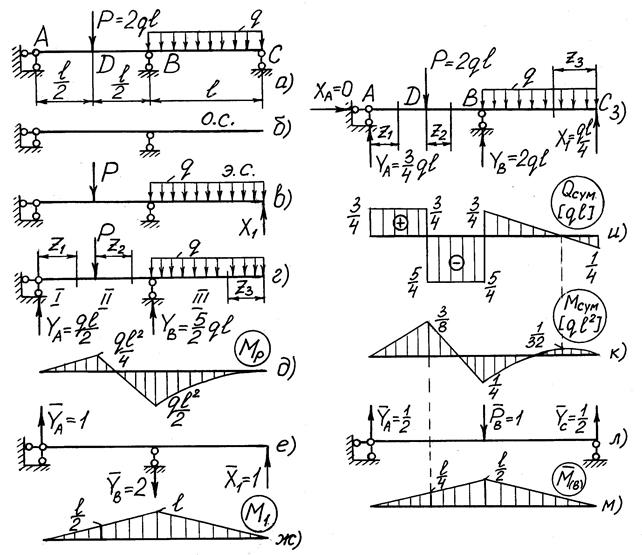Для получения ОС заданную систему освобождаем от всей нагрузки и связи в точке С. ОС показана на рис. 6б.

Рис. 6

Переходим к эквивалентной системе (ЭС).

Для этого ОС нагружаем заданной нагрузкой и неизвестной си­лой X_i в точке С. Эквивалентная система показана на рис. 6в.

Записываем каноническое уравнение

Для системы, один раз статически неопределимой, каноническое уравнение имеет вид

.

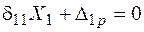Вычисляем коэффициенты уравнения.

Для этого строим грузовую M_p (рис. 6д) и единичную M₁ (рис. 6ж). Эпюры M_p и M₁ строят по стандартному алгоритму так, как это делали в контрольной работе № 1. Расчетные схемы для их построе­ния даны соответственно на рис. 6г,е. Для вычисления d₁₁ используем формулу (3.3а)

,

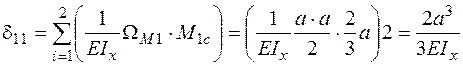здесь учтено, что результат перемножения эпюры M₁ самой на себя на участках I и II равны результату перемножения на участке III.

При вычислении 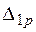перемножение эпюр M_p и M₁ на участках I и III выполнено по формуле (3.3а), на участке II по формуле (3.5).

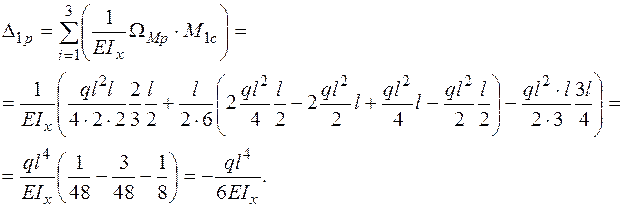Решаем каноническое уравнение.

Для этого d₁₁ и 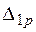сокращаем на общий множитель 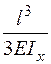и подставляем их в исходное уравнение

.

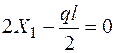Откуда .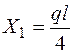

Строим суммарные эпюры.

Используем традиционный подход. Основную систему нагру­жаем заданной нагрузкой и найденной реакцией X₁ в точке С (рис. 6з). От их совместного действия по стандартному алгоритму (так, как это делали в контрольной работе № 1) строим суммарные эпюры.

Определяем опорные реакции

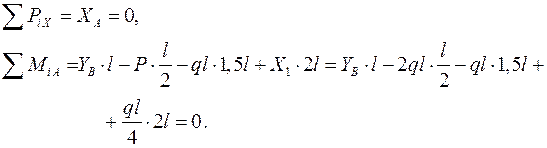откуда Y_B =2 ql.

.

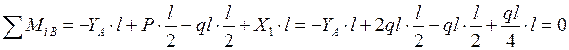откуда .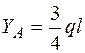

Проверка: .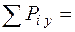

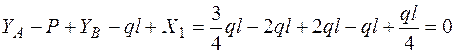Реакции определены верно.

Записываем аналитические выражения для определения Q и М.

I участок (0 £ z₁ £ )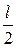

;

.

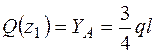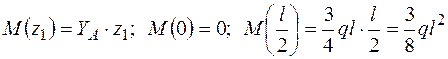II участок (0 £ z₂ £ )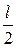

;

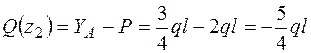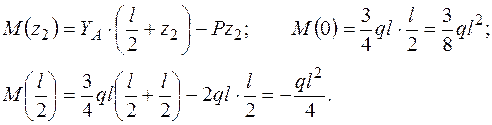
III участок (0 £ z £ l)

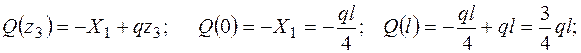
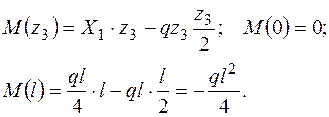
Так как Q на границах участка имеет разные знаки, то на эпюре М, в сечении, где Q = 0, будет экстремум. Определим его:

.

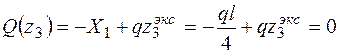Отсюда 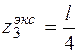. Подставляя значение 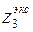в выражение М (z ₃), получаем:

.

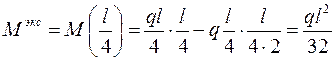По вычисленным значениям Q и M строим суммарные эпюры (рис. 6и,к).

Деформационная проверка

Берем иную ОС, чем та, с использованием которой выполнялось решение. Для этого в точке В убираем опору. Вместо нее прикладываем единичную вертикальную силу 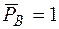(рис. 6л). От ее действия строим единич­ную эпюру 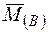(рис. 6м).

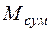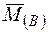Перемножаем эпюры и по формуле (3.5)

.

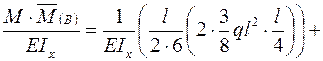
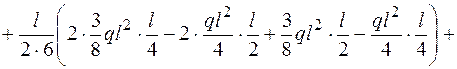
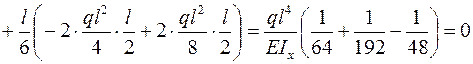Это показывает, что все действия по построению суммарных эпюр выполнены правильно.

2. Определяем для балки необходимый номер двутавра из условия прочности.

Условие прочности:

,

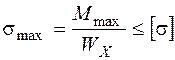где M _max – максимальный момент на эпюре М_{сум ,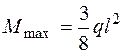}, ; W_x – момент сопротивления изгибу относительно оси х.

Из условия прочности определяем необходимый W_x

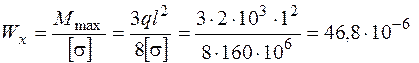м³ = 46,8 см³.

По сортаменту подходит двутавр № 12, у которого W_x = 58,4 см³.

3. Определяем для балки необходимый номер двутавра из заданного ус­ловия жёсткости.

Условие жёсткости .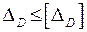

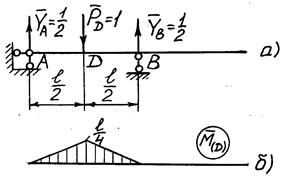
Выразим 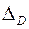– вертикальное перемещение (прогиб) в точке D. Для этого к основной системе в точке D прикладываем вертикальную единичную силу 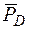(рис. 7а). Строим единичную эпюру изги­бающих моментов 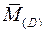(рис. 7б).

Перемножая эпюры М_сум (рис. 6к) и 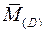по формуле (3.5), получаем выра­жение для .

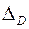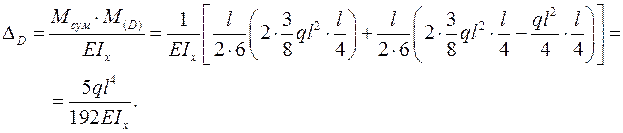
Подставляя найденное выражение для 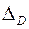в условие жесткости, по­лучим

.

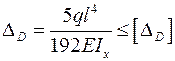Отсюда минимальное значение I_х для балки

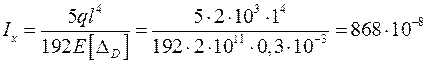м⁴ = 868 см⁴.

По сортаменту подходит двутавр № 16 с I_х = 873 см⁴.

Окончательно для балки из двух найденных двутавров берем боль­ший – двутавр № 16. Для него из таблиц сортамента: I_x = 873 см⁴, W_x = 109 см³, 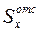= 109 см³, d = 5 мм.

4. Проверяем прочность балки по касательным напряжениям.

Условие прочности: .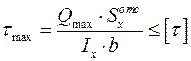

Q_max = 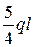(взято с эпюры Q_сум),

b = d.

Тогда

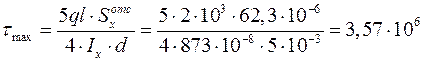Па =

= 3,57 МПа < [t] = 100 МПа.

Прочность балки по касательным напряжениям обеспечена.