Маршруты и циклы

Маршрутом в графе называют связную чередующуюся последовательность вершин и ребер (дуг), которая начинается и заканчивается вершиной, причем каждая соседняя пара – вершина и ребро (дуга), инцидентны друг другу.

Маршрут можно указать также перечислением вершин или ребер (дуг). Каждая пара соседних вершин или ребер (дуг) в таком представлении должны быть смежными.

В графе рис. 2.18 маршрут из точки “ a ” в точку “ b ” (а – начальная вершина, b – конечная вершина): последовательность вершина a,дуга e ₇, вершина d, дуга e ₆, вершина e, дуга e ₅, вершина c, ребро e ₃, вершина b.

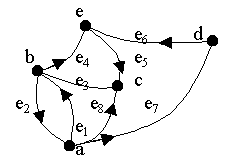
Рисунок 2.18

Число ребер (дуг) в маршруте называется его длиной.

Маршрут называется цепью, если все его ребра (дуги) различны и простой цепью, если все его вершины различны.

Ориентированную цепь (цепь, состоящую только из дуг, имеющих одинаковое направление) в орграфе называют путем.

Замкнутую цепь называют циклом, если ее длина >2. Цикл называется простым, если все его вершины различны.

Замкнутый путь называют контуром, если его длина >2. Контур называется простым, если все его вершины различны.

В графе на рис. 2.19 маршрут b–e ₁ –c–e ₂ –d–e ₅ –b является замкнутым и его вершины (b, c, d) и ребра (e ₁, e ₂, e ₅) различны, а длина маршрута равна 3, следовательно, данный маршрут можно назвать простым циклом.

Рисунок 2.19

Неорграф, в котором, перемещаясь от вершины к вершине по ребрам, можно попасть в каждую вершину, называется связным. В противном случае граф называется несвязным.

Граф G ₁(4,5) на рис. 2.20 связный. Он имеет одну компоненту связности. Несвязный граф G ₂(6,4) на рис. 2.20 состоит из двух компонент связности.

Орграф связен, если связен неорграф, полученный из него заменой дуг на ребра.

Орграф называется сильно связным, если любые его вершины взаимно достижимы. Вершина y достижима из вершины x, если имеется путь от x до y.

Заметим, связный неорграф всегда сильно связен.

Рисунок 2.20

Связный орграф слабо связен, если в нем существуют пары вершин с односторонней связью. Примеры сильно связного и слабо связного графов показаны на рис. 2.21.

Вершинной связностью графа называется наименьшее число вершин, удаление которых приводит к несвязному графу или нуль–графу, т.е. графу из одних вершин.

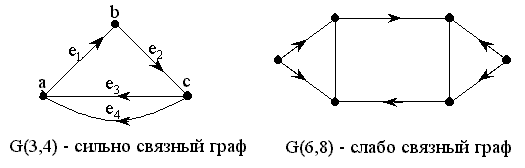
Рисунок 2.21

Вершинная связность графа G (7,7) рис. 2.22 для получения нуль графа равна 2 (результат удаления вершин c и e показан на рис. 2.23, а).

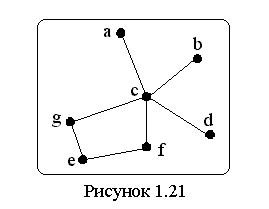
Рисунок 2.22

Вершинная связность графа G (7,7) для получения несвязного графа равна 1 (результат удаления вершины c показан на рис. 2.23, б).

Рисунок 2.23

Реберная (дуговая) связность определяется как наименьшее число ребер (дуг), удаление которых приводит к несвязному или нуль графу.

Вершина графа, удаление которой увеличивает число компонент связности, называется точкой сочленения, ребро с таким же свойством называется мостом.

На рис. 2.24 показан граф, имеющий мост и три точки сочленения:

вершины x ₃, x₄, x ₆ – точки сочленения, ребро x ₃, x ₄ – мост.

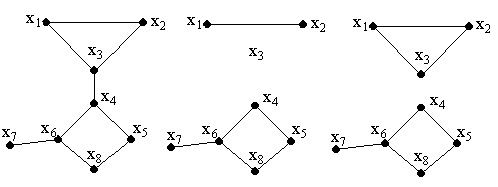
Рисунок 2.24