2015-05-14
999
Иногда требуется в разные цвета окрасить ребра графа так, чтобы смежные ребра имели разные цвета. Решить задачу о числе необходимых красок для такой раскраски ребер можно с помощью рассмотренных алгоритмов раскраски вершин графа. Для этого надо превратить ребра в вершины и соединить полученные вершины так, что две вершины соединяются ребром, если в исходном графе ребра были смежны.
Для реберной раскраски имеется достаточно точная оценка требуемого числа красок в виде
,
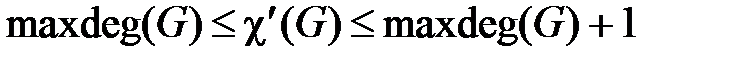где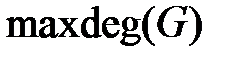 
максимальная степень вершин графа G.
Число красок, необходимое для реберной раскраски, при которой смежные ребра имеют разный цвет, обозначается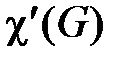 
и называется хроматическим классом или хроматическим индексом.
Для некоторых видов графов хроматический класс определяется достаточно просто, например, для графа в виде цикла с n вершинами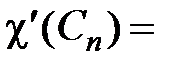 
2 или 3 в зависимости от того, четно n или нечетно. Для двудольных полных графов 
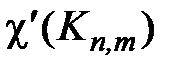= max(m, n). Для полных графов 
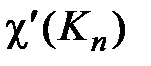= n, если n нечетно, и 
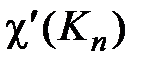= n – 1, если n четно.
