Минимальное покрытие двудольного графа

Покрытием двудольного графа G (X, Y, E) называется такое подмножество дуг W, что любая вершина графа инцидентна, по крайней мере, одной дуге из W (предполагается, что в графе нет изолированных вершин).

Например, для графа рис. 2.36 покрытием будет множество дуг

W = {(x ₁, y ₁), (x ₂, y ₄), (x ₃, y ₂), (x ₄, y ₃), (x ₅, y ₄), (x ₅, y ₅), (x ₆, y ₃)}.

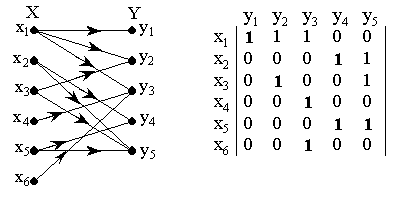
Рисунок 2.36

В матрице смежности, показанной на рис. 2.36, дуги множества W выделены полужирным шрифтом.

Анализируя эту матрицу, можно определить покрытие графа как такой набор единиц, что каждая строка и каждый столбец содержат, по крайней мере, по одному элементу из этого набора.

По условию задачи требуется найти такое покрытие W ₀, которое содержит минимальное количество дуг.

Алгоритм с использованием матрицы инцидентности графа

Для простоты будем рассматривать неориентированный двудольный граф, вершины которого обозначены натуральными числами 1, 2, 3,..., а ребра строчными буквами латинского алфавита.

Приведем шаги алгоритма:

1) Составляем матрицу инцидентности графа, в которой, как известно, число строк равно числу вершин графа, а число столбцов равно числу ребер графа. Каждое ребро инцидентно двум вершинам, поэтому в каждом столбце будет две единицы.

2) Для определения минимального покрытия вершин графа ребрами необходимо найти такую минимальную совокупность столбцов матрицы инцидентности (ребер), которая содержала хотя бы по одной 1 во всех строках, т.е. могла бы покрыть каждую вершину графа.

Для этого для каждой вершины (для каждой строки) записываем логическую сумму имен ребер, инцидентных вершине (имеющих 1 в строке вершины). Каждая сумма символизирует тот факт, что для покрытия вершины, чьим именем обозначена строка, нужно или ребро a, инцидентное вершине, или ребро b, инцидентное вершине, и т.д.

3) Для покрытия графа надо покрыть и вершину 1, и вершину 2, и т.д. Поэтому из сумм предыдущего пункта, заменив союз И символом логического умножения, составляем логическое произведение.

4) полученное логическое произведение сумм преобразуется в дизъюнктивную форму и минимизируется. Терм с минимальным числом букв и будет представлять минимальное покрытие графа.

Алгоритм с использованием матрицы смежности графа

Рассмотрим алгоритм построения минимального покрытия двудольного графа на примере графа G (X, Y, E), показанного на рис. 2.37.

Матрица смежности графа показана в табл. 2.2. (размер матрицы 6 х 5: 6 = | X | = m – число вершин множества X, 5 = | Y | = n – число вершин множества Y).

Приведем шаги алгоритма:

1) Сопоставим каждой строке матрицы смежности графа число F_i, равное сумме ее элементов, и каждому столбцу – число G_j, равное сумме его элементов (соответствующие числа показаны справа и снизу таблицы).

Очевидно, что

.

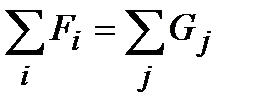2. Если

,

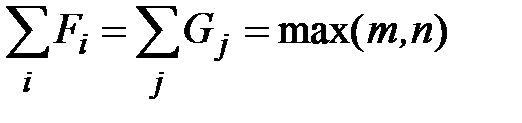то множество дуг, соответствующих 1, дает минимальное покрытие.

Рисунок 2.37

Таблица 2.2

	y1	y2	y3	y4	y5	Fi
x1
x2
x3
x4
x5
x6
Gj

Если

,

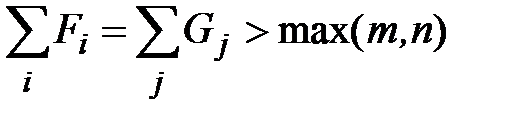то отмечаем последовательно в произвольном порядке символом * каждую из единиц, для которой F_i – 1>1 и G_j – 1>1, при этом F_i и G_j уменьшаем на 1.

Например, помечаем 1 на местах (x ₁, y ₁), (x ₂, y ₃), (x ₅, y ₄) в матрице табл. 24.2, получим матрицу, показанную в табл. 2.3.

Видим, эту операцию нельзя продолжить.

3. В каждой строке с F_i >1 ищем такую неотмеченную 1, что в содержащем ее столбце k найдется отмеченная 1, в строке m которой есть либо неотмеченная 1 с G_j > 1, либо отмеченная 1.

Если найдена 1 с G_j > 1, то есть возможность увеличить число 1 с метками. Для этого помечаем найденную единицу с координатами m, j и единицу с координатами i, k.

Метку у единицы c координатами k, m удаляем. Из F_i и G_j вычитаем по 1.

Если в строке m найдена отмеченная единица в столбце j c G_j = 1 и этот столбец содержит также отмеченyю 1 в строке n, то в строке n ищем либо неотмеченную 1 с G_j > 1, либо отмеченную 1 и т.д.

Если, действуя по этому алгоритму, невозможно больше отметить 1, то единицы без меток дают минимальное покрытие.

Таблица 2.3

	y1	y2	y3	y4	y5	Fi
x1	1*
x2			1*				m
x3							i
x4
x5				1*
x6
Gj
		j	k

В рассматриваемом примере последовательно получаем табл. 2.4 и табл. 2.5. В табл. 2.3, 2.4 и 2.5 пути поиска выделены полужирным шрифтом.

Таблица 2.4

	y1	y2	y3	y4	y5	Fi
x1	1*
x2		1*
x3			1*				i
x4
x5				1*			m’
x6
Gj
	j’			k’

Таблица 2.5

	y1	y2	y3	y4	y5	Fi
x1	1*
x2		1*
x3			1*	1*			i
x4
x5	1*						m’
x6
Gj
	j’			k’

Минимальное покрытие графа будет таким

W ₀ = {(x ₁, y ₂), (x ₂, y ₃), (x ₃, y ₅), (x ₄, y ₁), (x ₅, y ₄), (x ₆, y ₁)}.

Рассмотрим двудольный граф G (X, Y, E) и два таких подмножества 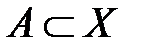и 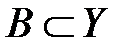, что | A | = | B |.

Взаимно однозначное отображение A на B называется паросочетанием отображающим A в Y или A на B. На языке графов паросочетание – это подмножество несмежных ребер (дуг) двудольного графа.