Остов графа

Остов – минимальное множество ребер, которые связывают все вершины связного графа.

Остов это дерево. Часть G ' графа G называется остовом (каркасом, скелетом), если V ’ = V и все они связаны без циклов. Остов обычно обозначают буквой T. Для орграфов остов – часть G, которая является остовом в неорграфе, полученном из G удалением ориентации дуг.

Остов получается из графа разрушением циклов. Число удаляемых при этом ребер: 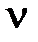(G) = m – n + 1 – называется цикломатическим числом или цикломатическим рангом графа (или просто рангом графа).

Если граф состоит из нескольких компонент, то его остов лес, а число удаляемых при определении остова ребер будет равно:

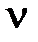(G) = m – n + ρ,

где ρ – количество компонент связности графа.

Количеств ребер в остове графа:

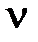*(G) = n – ρ

называется коциклическим рангом.

(У связного графа 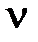*(G) = n – 1.)

Для дерева цикломатическое число равно 0.

Нахождение остова минимальной длины

Имеется связный граф G (V, E):

1) Строим начальный остов T_i, который состоит из всех вершин и одного ребра с минимальным весом.

2) Имеем T_i, среди всех ребер находим ребро с минимальным весом такое, которое смежно с одним из ребер из T_i и которое не образует циклов. Добавляем его к T_i.

3) Повторяем п. 2, пока находятся нужные ребра.

Фундаментальным циклом графа G (V, E) с остовным деревом T (V, E ') называется простой цикл, получаемый в результате добавления к T одного из ребер G, не принадлежащего E '. Количество фундаментальных циклов графа G = (V, E) при любом остовном дереве T равно цикломатическому числу 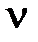(G).

Пусть G (V, E) связный неорграф с n вершинами и m ребрами, T – остов графа, имеющий n – 1 ребро, которые называются ветвями T (ведь остов – это дерево) и обозначаются b_j.

Не входящие в остов 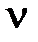(G) = m – n + 1 ребер называются хордами и обозначаются h_i.

Если к дереву T добавить произвольную хорду h_i, то образуется точно один цикл C_i. Этот цикл состоит из хорды h_i и некоторых ветвей остова, образующих простую цепь и соединяющих вершины хорды h_i.

Цикл C_i называется фундаментальным циклом графа G относительно хорды h_i остова T (в общем случае остовов в графе может быть много). Таким образом, фундаментальный цикл содержит точно одну хорду остова графа.

Множество всех фундаментальных циклов { C ₁, C ₂, …, C _i, …, C_{m – n +1}} относительно хорд остова T называется фундаментальным множеством циклов графа G. Мощность этого множества равна цикломатическому числу 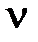(G) = m – n +1 или рангу графа G.

фундаментальное множество циклов графа можно задать с помощью матрицы, строки которой имеют вид

h ₁, h ₂, …, h_{m – n +1}, b ₁, b ₂, …, b_{n –1},

где h_i, b_j – хорды и ветви соответственно.

В каждом цикле имеется одна хорда h_i и некоторое множество ветвей остова T. Этой хорде h_i и ветвям, входящим в цикл C_i, присвоим значение 1, остальным ребрам графа присвоим значение 0. Повторяя процедуру для всех хорд, получим матрицу строк из 0 и 1.

Разрезом неорграфа G (V, E) по разбиению множества вершин V на два подмножества V ₁ и V ₂ называется множество ребер, соединяющих вершины из подмножества V ₁ с вершинами подмножества V ₂. В связном графе любой разрез не пуст.

Непустой разрез K неорграфа G называется простым или коциклом, если множество ребер K не содержит разрезов G ни по какому разбиению (любой разрез разбивает граф на две части – увеличивает число компонент связности).

В связном неорграфе остов T имеет, по крайней мере, одно общее ребро с любым разрезом графа.

В связном неорграфе любой цикл имеет с любым разрезом, проходящим через ребра цикла, четное число ребер.

Пусть имеем связный неорграф G с остовом T. И пусть b ₁, b ₂, …, b_i,…, b_{n –1} – ветви остова T.

Удаляя произвольную ветвь b_i из T, получаем лес с двумя компонентами, т. е. каждое ребро b_i есть разрез T по некоторому разбиению вершин V ₁, V ₂.

В графе могут найтись еще какие–то ребра h_{i 1}, h_{i 2},…, h_ij, которые соединяют V ₁ и V ₂.

Множество ребер K_i = { b_i, h_{i 1}, …, h_ij } образует разрез G относительно ветви b_i, который называют фундаментальным разрезом относительно b_i остова T. Таким образом, фундаментальный разрез содержит точно одну ветвь остова графа.

Множество { K ₁, K ₂, …, K_{n –1}} всех фундаментальных разрезов графа G называется фундаментальным множеством разрезов графа G относительно остова T.

Мощность этого множества равна 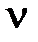*(G) = n –1. (В общем случае n – 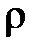, где 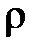число компонент связности графа.)

По аналогии с фундаментальными циклами, каждому фундаментальному разрезу можно поставить в соответствие вектор

(a_{i 1}, a_{i 2}, …, a_im),

где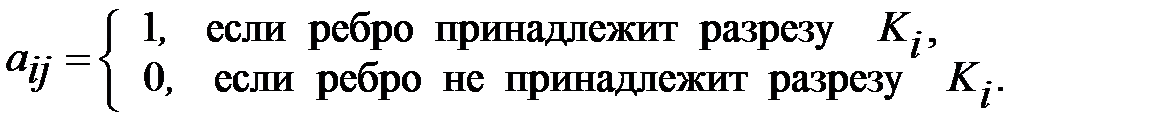

Из этих векторов можно составить матрицу фундаментальных разрезов.

Поскольку каждый фундаментальный разрез содержит точно одну ветвь T, то матрица K имеет вид:

		hi,j – хорды	bi – ветви T
	K 1	h 1,1	.	h 1,V*				.
K =	.	h 2,1	.	h 2,V*				.
	.	.	.	.	.	.	.	.	.
	K V*	h V*,1	.	h V*,V*				.

где v* это 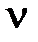*(G) = n – 1.

Таким образом 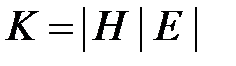, где H – матрица хорд графа, E – единичная матрица порядка *(G).

Матрицы фундаментальных циклов C и фундаментальных разрезов K взаимосвязаны.

Если 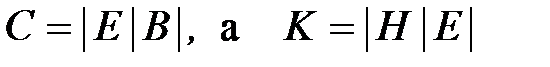, то ,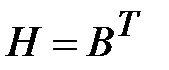

где 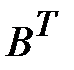– транспонированная матрица B.

Следовательно, для анализа графа достаточно найти одну матрицу (C или K), а другую можно определить транспонированием.

Планарные графы

Планарный граф – это граф, допускающий укладку на плоскости, т.е. он может быть изображен на плоскости так, что никакие ребра не имеют общих точек, кроме своих вершин. Изображение графа на плоскости с соблюдением этого условия называется плоским графом.

Планарность нужна, например, для реализации печатного монтажа, в процессе разработки которого схема устройства представляется в виде графа: элементы – вершины, связи между выводами элементов – ребра.

Если граф не планарен, то приходится удалять (переносить на другой слой, на другую плоскость) отдельные ребра. Минимальное число ребер, которое надо удалить для получения плоского изображения, называется числом планарности графа и обозначается (G). Для полных графов с

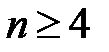
(K_n) = (n –3)(n –4)/2.

Из формулы следует, что при n = 4 (K ₄) = 0. Для K ₅ (K ₅) = 1, следовательно, чтобы граф K ₅ стал плоским, из него надо удалить одно ребро.

При перенесении на вторую плоскость, перенесенная часть может опять оказаться не плоской. Тогда отдельные ребра переносят на новую плоскость и т.д. Минимальное число плоскостей, при котором граф разбивается на плоские части, называется толщиной графа и обозначается t (G).

Толщина произвольного графа удовлетворяет неравенству

t (G) .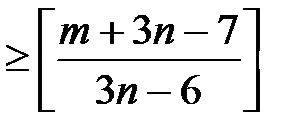

Здесь [ x ] – целая часть x.

Толщина полных графов удовлетворяет неравенству

t (K_n) .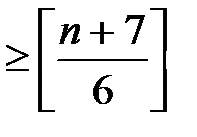

Например, для K ₅ t (K ₅) = 2.

Ответ на первый вопрос: – Граф планарен? – можно получить, если воспользоваться условиями планарности.

У связного плоского графа с n 3 число ребер m удовлетворяет условию

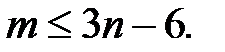
У связного плоского двудольного графа

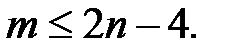
У плоского графа кроме вершин и ребер можно выделить еще один геометрический образ – грань. Область плоскости, ограниченная ребрами связного плоского графа и не содержащая внутри себя ни ребер, ни вершин, называется его гранью. Внешняя неограниченная грань называется бесконечной гранью. У графа без циклов ровно одна грань – бесконечная. Не следует думать, что она какая–то исключительная. При укладке графа на сферу эта грань ничем не будет отличаться от других.

Число граней f в связном плоском графе определяется из соотношения:

f = m – n + 2,

где n – число вершин, m – число ребер.

Пусть задана часть G ₁ = (V ₁, E ₁) графа G = (V, E).

Будем называть кускомграфа G относительно G ₁:

1) ребро 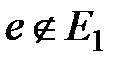вместе с его концами,которые принадлежат V ₁,

2) а также компоненту связности G’_i = (V’_i, E’_i) подграфа, порожденного подмножеством вершин V \ V _l, дополненную всеми ребрами, инцидентными вершинам из V'_i, и всеми вершинами этих ребер, принадлежащими V ₁, которые называются «контактными точками»;

Алгоритм использует последовательный процесс присоединения к некоторому плоскому подграфу цепи 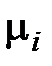, оба конца которой (и только они) – вершины . Эта цепь разобьет одну из граней на две.

В качестве начального плоского графа 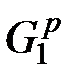выбирают некоторый цикл графа G. Чтобы перейти от подграфа к 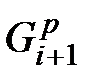, предварительно рассматривают все куски P_j графа G относительно .Грань f_k графа и кусок Р_j совместимы, если все его контактные точки принадлежат множеству вершин этой грани.

Для каждого куска определяем грани, которые с ним совместимы. Возможны три случая:

1) Некоторый кусок не совместим ни с какой гранью графа . Тогда граф не плоский.

2) Какой–либо кусок совместим с единственной гранью f_k графа . Тогда выберем в этом куске цепь 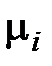такую, что оба ее конца (и только они) принадлежат . Дополняя ребрами и вершинами этой цепи, получаем 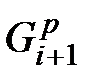, проводя 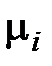внутри грани f_k.

3) Если каждый из кусков Р_j совместим, по крайней мере, с двумя гранями графа , то можно выбрать цепь 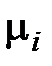в любом из кусков и действовать как в случае 2.