2015-05-14
761
Если для любой вершины xi выполняется условие
,
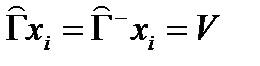то граф сильно связен.
Поскольку связный неорграф всегда сильно связен, то полученный алгоритм определения компонент сильной связности пригоден и для определения компонент связности неорграфов: Каждая компонента неорграфа сильно связана, а между компонентами связи нет.
Связность орграфа проверяется удалением ориентации дуг и установлением связности полученного неорграфа.
Дан граф рис. 2.34, для которого имеем
A = 
.
Рисунок 2.34
В графе изолированных вершин нет, поэтому исключать ничего не надо.
Выберем вершину 1.
В графе 6 вершин, поэтому для определения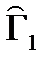 
и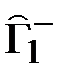 
нужно возводить первую строку и первый столбец матрицы смежности в степени с первой по пятую.Возводим в степень первую строку матрицы A (сложение и умножение элементов булевские)
Первая строка матрицы смежности
= 
.
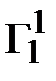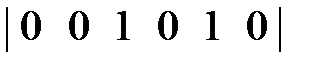Вторая степень первой строки матрицы смежности:
= * = 
.
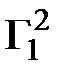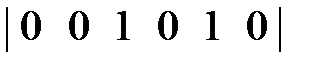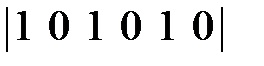Третья степень первой строки матрицы смежности:
= 
* = .
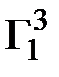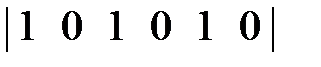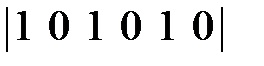При возведении в третью степень получено повторение строки, возводимой в степень, поэтому операцию возведения в степень прекращаем.
Если продолжить возведение в степень, то результат будет повторяться.
Найдем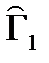 
.
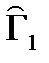= {1} 
=
= 
= .
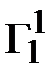
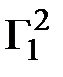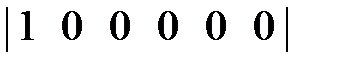
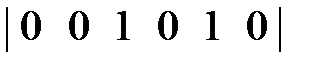
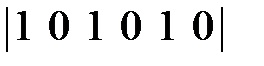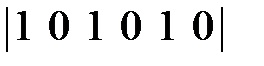В других обозначениях
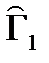= {1, 3, 5}.
Определим .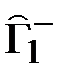
= 
. 
= * = 
.
= 
* = .
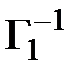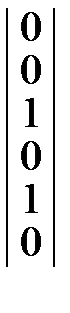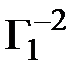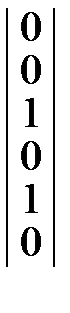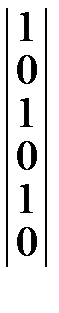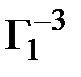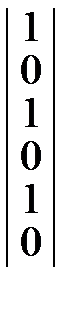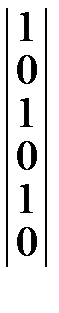Результат совпадает с начальным значением, следовательно, возведение в степень надо прекратить.
Найдем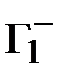 
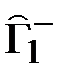= {1} = 
= .
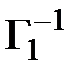
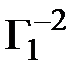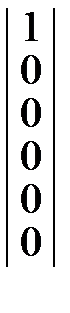
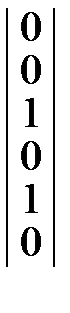
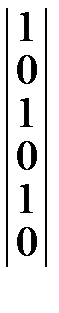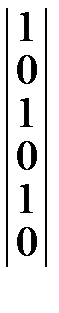В других обозначениях
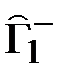= {1, 3, 5}.
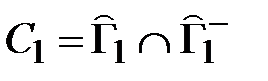= {1, 3, 5} 
{1, 3, 5} = {1, 3, 5}.
Вершины 1, 3, 5 принадлежат отдельной компоненте связности, поэтому на дальнейший процесс поиска других компонент связности влиять не будут. для уменьшения объема вычислений эти вершины, вместе с инцидентными им ребрами, можно исключить. Рассматриваемый пример достаточно простой, поэтому исключать ничего не будем.
Возьмем вершину, не принадлежащую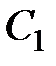 
, например, 4.
Действуя аналогично, находим
= 
.
= * = 
.
= 
* = 
.
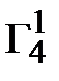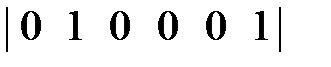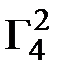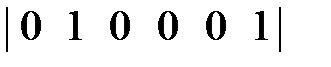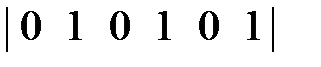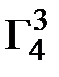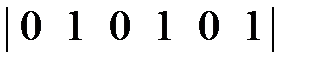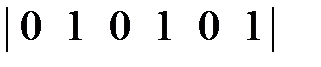Получено повторение строки, возводимой в степень, поэтому операцию возведения прекращаем.
Найдем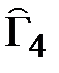 
.
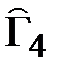= {4} 
=
= 
= 
.
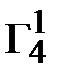
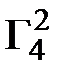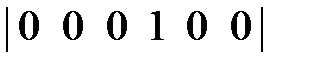
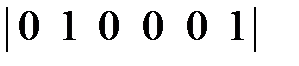
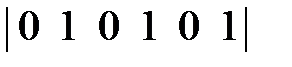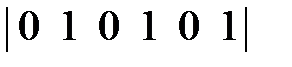В других обозначениях
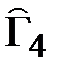= {2, 4, 6}.
Определим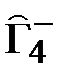 
.
= 
. 
= * = 
.
= * = .
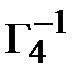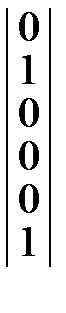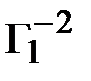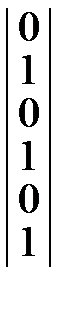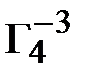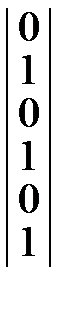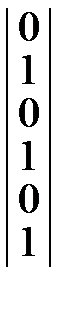Результат совпадает с начальным значением, следовательно, возведение в степень надо прекратить.
Найдем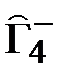 
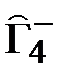= {4} 
= 
= .
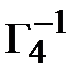
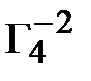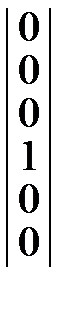
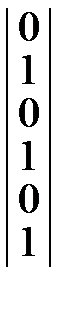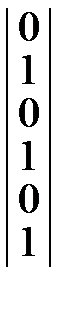В других обозначениях
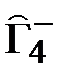= {2, 4, 6}.
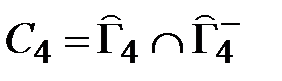= {2, 4, 6} {2, 4, 6} = {2, 4, 6}.
Таким образом, все вершины графа вошли в два класса – в две компоненты связности C 1 = {1, 3, 5} и C 4 = {2, 4, 6}.
