Численность, возрастная структура, биотический потенциал и динамика популяций. Жизненные циклы. Логистическое уравнение. Регуляция роста популяций

Вероятно, наиболее общим правилом является то, что индивиды любого вида живого всегда представлены не изолированными отдельностями, а их определенным образом организованными совокупностями. Это правило получило имя С. С. Четверикова, сформулировавшего его в 1903 г. Его можно назвать правилом объединения в популяции. В связи с тем, что любая популяция обладает строго определенной генетической, фенотипической, половозрастной и другой структурой, она не может состоять из меньшего числа индивидов, чем необходимо для обеспечения стабильной реализации этой структуры и устойчивости популяции к факторам внешней среды. Именно в этом состоит принцип минимального размера популяций. Такой размер не есть константа для любых видов, он строго специфичен для каждой популяции. Выход за пределы минимума чреват для популяции гибелью: она уже не будет в состоянии самовозобновиться.

Оно носит название теории биоценотической регуляции численности популяции К. Фридерихса (1927): регуляция численности популяции есть результат комплекса воздействий абиотической и биотической среды в местообитании вида. Совершенно очевидно — теория К. Фридерихса объясняет, что лимитирует и формирует потенцию роста численности популяции, заложенную генетически. Однако, как известно, бывают взрывы роста численности популяций — сбои в регуляторных системах самоограничения и внешних ограничений популяционного роста.

правило увеличения видового разнообразия по мере продвижения с севера на юг, или правило Уоллеса. Оно касается как видов, так и составляемых ими сообществ: в тропиках значительно больше абсолютное число видов, чем на Севере, и в составе южных сообществ их также намного больше.

Хорошо известны модели роста популяций, которые основаны на предположении пропорциональности скорости роста численности популяции. Впервые такое поведение популяции было описано Томасом Мальтусом (1798 г.) в виде закона о неограниченном экспоненциальном росте:, 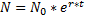(5.1) где 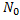– начальная численность популяции; r – коэффициент скорость роста, часто выражается в процентах за год. Для большинства популяций существуют ограничивающие факторы, при которых рост прекращается. Единственным исключением является человеческая популяция, которая на протяжении исторического времени растет даже быстрее, чем по экспоненте.

Одной из причин ограничения роста может быть недостаток пищи. Базовой моделью, описывающей ограниченный рост, является модель Ферхюльста (1848 г.)., 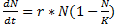(5.4) гдеN – размер популяции, а K – максимально возможная в данных условиях численность популяции (потенциальная емкость экологической системы).

Наличие определенной емкости среды, ограничивающей рост популяции, является важной экологической закономерностью. Множитель (1-n/k) часто называют сопротивлением окружающей среды. Решение уравнения (5.4) имеет вид: N= 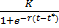(5.5) где 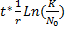соответствует моменту времени, когда численность популяции достигнет величины N= K/2.