В гидроаэромеханике используется единый подход к изучению жидкостей и газов. Жидкости и газы рассматривают как сплошные среды, не вдаваясь в их молекулярное строение. Жидкость считается несжимаемой, поскольку ее плотность мало зависит от давления. Однако, как показывают расчеты, при движении газов со скоростями, намного меньшими скоро- сти звука в этой среде, их также можно с достаточной точностью считать несжимаемыми. Движение жидкости (газа) называется течением, а совокупность движущихся частиц жидкости – потоком.
Графически движение жидкости изображается с помощью линий тока, которые проводятся так, что касатель- ные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис.1.14.а). Часть жидкости, ограниченную линиями тока, называют трубкой тока (рис.1.14.в).
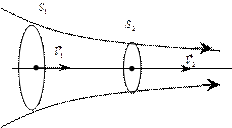

а) в)
Рис.1.14
Течение жидкости называется стационарным (устано- вившимся), если значение скоростей в каждой ее точке со временем не меняется. Для стационарного течения несжима- емой жидкости справедливо соотношение
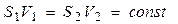 . (1.79)
. (1.79)
Следовательно, при стационарном течении произведе ние скорости течения на поперечное сечение трубки тока есть величина постоянная. Это соотношение называется уравне- нием неразрывности.
Жидкость, у которой полностью отсутствуют силы внутреннего трения, называeтся идеальной. Течение идеальной жидкости не сопровождается диссипацией энергии.
Применение закона сохранения механической энергии к установившемуся течению жидкости позволяет получить соотношение
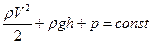 . (1.80)
. (1.80)
Это уравнение называется уравнением Бернулли.
Величина 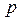 в формуле называется статическим давле- нием, величина
в формуле называется статическим давле- нием, величина 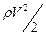 - динамическим давлением (напором), а величина
- динамическим давлением (напором), а величина 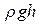 - гидростатическим давлением.Для горизон- тальной трубки выражение (1.80) принимает вид
- гидростатическим давлением.Для горизон- тальной трубки выражение (1.80) принимает вид
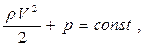 (1.81)
(1.81)
где 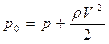 - полное давление.
- полное давление.
Из формул (1.79) и (1.81) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в широких местах, т.е. там, где скорость меньше.
Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого имеется малое отверстие (рис.1.15).
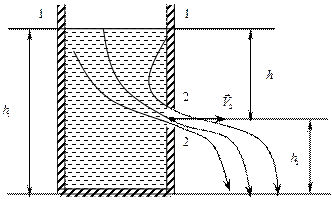
Рис.1.15
Напишем уравнение Бернулли для сечений на уровне 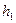 и
и 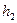 :
:
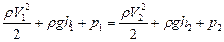 . (1.82)
. (1.82)
Так как давления 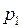 и
и 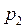 в жидкости на уровнях первого и второго сечений равны атмосферному, т.е.
в жидкости на уровнях первого и второго сечений равны атмосферному, т.е. 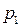 =
= 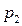 , то уравне- ние будет иметь вид
, то уравне- ние будет иметь вид
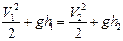 . (1.83)
. (1.83)
Из уравнения неразрывности (1.79) следует, что 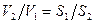 , где
, где 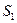 и
и 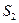 - площади поперечных сечений сосуда и отверстия. Если
- площади поперечных сечений сосуда и отверстия. Если 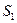 >>
>> 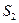 , то
, то 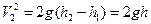 , или
, или
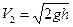 . (1.84)
. (1.84)
 2015-05-14
2015-05-14 6144
6144
