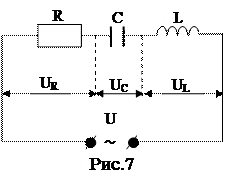
 Предположим, что цепь электрического тока, элементы которой соединены по схеме рис.7. Пусть возникший ток изменяется по закону
Предположим, что цепь электрического тока, элементы которой соединены по схеме рис.7. Пусть возникший ток изменяется по закону
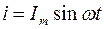 (6)
(6)
тогда на отдельных элементах цепи напряжения будут изменятся по следующим законам:
на активном сопротивлении - 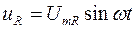
на индуктивном сопротивлении - 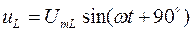
на емкостном сопротивлении - 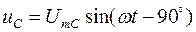
на концах всей цепи - 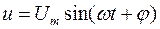
где j - сдвиг фаз между i и u
Т.к. алгебраическая сумма мгновенных значений напряжений на отдельных элементах цепи равна мгновенному напряжению всей цепи 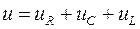 , то амплитудные значения напряжений складываются геометрически:
, то амплитудные значения напряжений складываются геометрически: 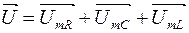 . Эффективные напряжения также складываются
. Эффективные напряжения также складываются
 | |||
 | |||
геометрически:
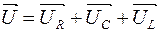 (смотрите рис.8).
(смотрите рис.8).
Рис. 8. Рис. 9.
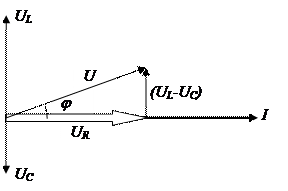
Построим векторную диаграмму. Сначала из точки "0" проведем вектор эффективного тока 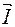 . Пусть
. Пусть 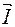 горизонтален. Тогда UR совпадает по фазе. Вектор
горизонтален. Тогда UR совпадает по фазе. Вектор 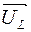 проводим перпендикулярно в сторону опережения. Вектор
проводим перпендикулярно в сторону опережения. Вектор 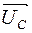 проводим под углом 90° в сторону отставания от тока. Чтобы найти
проводим под углом 90° в сторону отставания от тока. Чтобы найти 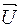 надо произвести геометрическое сложение как показано на чертеже.
надо произвести геометрическое сложение как показано на чертеже.
Из векторной диаграммы видно, что 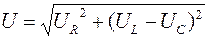 т.к.
т.к. 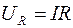 ,
, 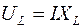 ,
, 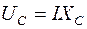 то
то 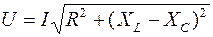 .
.
Отсюда получаем обобщенный закон Ома для последовательной цепи переменного тока
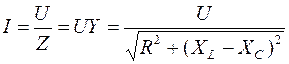 (16)
(16)
где I и U эффективные значения тока и напряжения
Z – полное сопротивление (импеданс)
Y – полная проводимость (адмитанс)
Очевидно 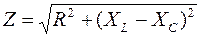 (17)
(17)
Из векторной диаграммы (рис.8) также видно, что разность фаз между напряжением и током можно определить из уравнений:
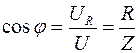 (18)
(18)
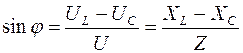 (19)
(19)
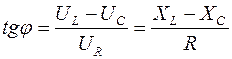 (20)
(20)
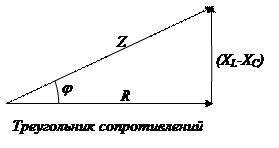
Иногда удобно строить для расчетов треугольник сопротивлений (рис. 9).
R – активное сопротивление
(XL–XC) – реактивное сопротивление
Z – импеданс
Активная мощность в этом случае выразится уравнением 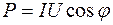 .
.
Из уравнения (16) видно, что при XL=XC – условие резонанса, Z*=R, 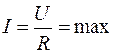 , UL=UC, U=UR – т.е. имеет место резонанс напряжений. При этом j*=0, т.к. R=Z.
, UL=UC, U=UR – т.е. имеет место резонанс напряжений. При этом j*=0, т.к. R=Z.
 2015-05-14
2015-05-14 699
699








