Т.С. Китаева
«Определение ускорения свободного падения
При помощи физического маятника»
Методические указания к выполнению лабораторной работы № 14
по курсу механики, молекулярной физики и термодинамики.
Калуга 2006 г.
Цель работы: определение ускорения свободного падения при помощи физического маятника.
Теоретическая часть.
Колебаниями называются процессы, характеризующиеся той или иной степенью повторяемости во времени.
Системы, совершающие колебания, называются колебательными: математический маятник, крутильный маятник, физический маятник и др.
В зависимости от характера воздействия на колеблющуюся систему различают свободные и вынужденные колебания.
Свободными (или собственными) называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как она была выведена из состояния равновесия.
Колебания называются периодическими, если значения характеризующих их физических величин повторяются через одинаковые промежутки времени.
|
|
|
Простейшими свободными периодическими колебаниями являются гармонические - то есть колебания, при которых физические величины, их характеризующие, изменяются по закону синуса или косинуса.
Пусть колебательная система совершает гармонические колебания. Согласно основному уравнению динамики поступательного движения имеем:
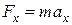 , (1)
, (1)
где 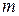 - масса колебательной системы;
- масса колебательной системы;
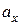 - ускорение колебательной системы вдоль оси
- ускорение колебательной системы вдоль оси 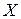 ,
, 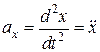 .
.
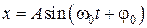 , (2)
, (2)
где 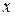 - смещение колебательной системы относительно положения равновесия;
- смещение колебательной системы относительно положения равновесия;
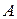 - амплитуда колебаний, равная максимальному абсолютному значению смещения;
- амплитуда колебаний, равная максимальному абсолютному значению смещения;
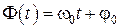 - фаза колебаний - аргумент тригонометрической функции в формуле (2);
- фаза колебаний - аргумент тригонометрической функции в формуле (2);
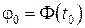 - начальная фаза колебаний - значение фазы колебаний в начальный момент времени
- начальная фаза колебаний - значение фазы колебаний в начальный момент времени 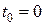 ;
;
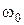 - круговая (циклическая) собственная частота колебаний;
- круговая (циклическая) собственная частота колебаний;
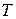 - период колебаний - наименьший интервал времени, по истечении которого значения физических величин, характеризующих колебания, повторяются.
- период колебаний - наименьший интервал времени, по истечении которого значения физических величин, характеризующих колебания, повторяются.
То есть
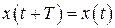 или
или 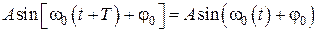 ,
,
при этом фаза колебаний будет отличаться на 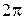 :
:
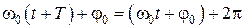 ,
,
откуда
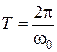 (3)
(3)
Продифференцируем выражение (2) дважды, найдём ускорение и подставим его в (1):
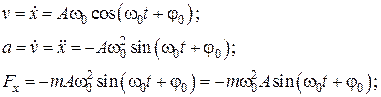
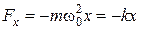 , (4)
, (4)
где 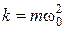 .
.
Видим, что сила 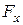 , действующая на колебательную систему, совершающую гармонические колебания, удовлетворяет следующим условиям:
, действующая на колебательную систему, совершающую гармонические колебания, удовлетворяет следующим условиям:
1. сила 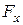 пропорциональна смещению х;
пропорциональна смещению х;
2. сила 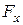 направлена к положению равновесия (возвращающая сила).
направлена к положению равновесия (возвращающая сила).
Роль такой силы может играть как упругая, так и квазиупругая сила.
Используя понятие квазиупругой силы, исходя из основного уравнения динамики поступательного движения для колебательной системы, имеем:
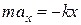 ,
,
где 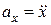 ;
;
|
|
|
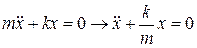 ,
,
где 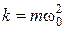 ;
;
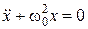 (5)
(5)
Выражение (5) есть дифференциальное уравнение гармонических колебаний, решением которого является выражение вида 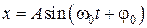 .
.
В качестве колебательной системы рассмотрим физический маятник - абсолютно твёрдое тело, совершающее колебания в вертикальной плоскости под действием силы тяжести вокруг неподвижной горизонтальной оси «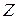 », не проходящей через центр масс «
», не проходящей через центр масс «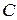 » (Рис. 1.).
» (Рис. 1.).
Если физический маятник массой «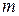 » отклонить на небольшой угол
» отклонить на небольшой угол 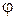 от положения равновесия, то момент силы тяжести относительно т. «
от положения равновесия, то момент силы тяжести относительно т. «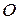 » можно представить:
» можно представить:
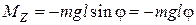 ,
,
где 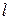 - расстояние от т. «
- расстояние от т. «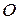 », лежащей на оси вращения, до центра масс «
», лежащей на оси вращения, до центра масс «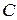 »; причём здесь учтено, что для малых углов
»; причём здесь учтено, что для малых углов 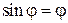 .
.
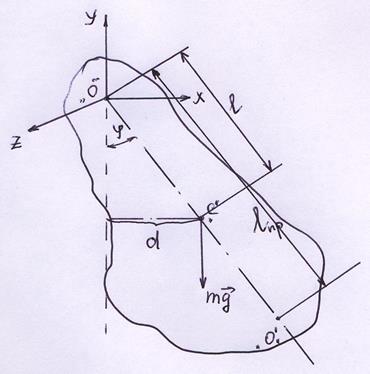
Рис. 1. Физический маятник.
Запишем основное уравнение динамики вращательного движения относительно неподвижной оси «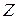 »:
»:
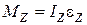 , (6)
, (6)
где 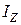 - момент инерции физического маятника относительно оси «
- момент инерции физического маятника относительно оси «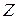 »;
»;
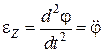 - угловое ускорение относительно той же оси «
- угловое ускорение относительно той же оси «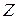 ».
».
Тогда уравнение (6) можно представить:
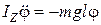 или
или 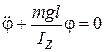 .
.
Введём обозначение 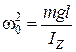 ,
,
тогда
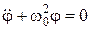 (7)
(7)
Уравнение (7) является дифференциальным уравнением свободных колебаний физического маятника, решением которого является уравнение гармонических колебаний с собственной круговой частотой 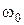 :
:
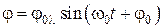 (8)
(8)
Период малых колебаний физического маятника равен:
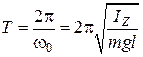 (9)
(9)
Введём понятие приведённой длины физического маятника.
С этой целью рассмотрим другую колебательную систему - математический маятник — материальная точка массой «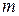 », подвешенная на невесомой нерастяжимой нити и колеблющаяся под действием силы тяжести в вертикальной плоскости.
», подвешенная на невесомой нерастяжимой нити и колеблющаяся под действием силы тяжести в вертикальной плоскости.
Хорошим приближением математического маятника является небольшой тяжёлый шарик, подвешенный на тонкой длинной нити (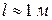 ).
).
Поскольку математический маятник можно представить как предельный случай физического маятника, учитывая, что его момент инерции относительно горизонтальной неподвижной оси, проходящей через точку подвеса, равен: 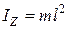 , получим следующее выражение для периода колебаний математического маятника:
, получим следующее выражение для периода колебаний математического маятника:
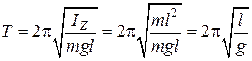 (10)
(10)
Сравнивая выражения (9) и (10), видим, что периоды малых колебаний физического и математического маятников будут равны в том случае, если длина математического маятника равна 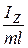 . Эта величина называется приведённой длиной физического маятника и обозначается
. Эта величина называется приведённой длиной физического маятника и обозначается 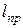 , то есть:
, то есть:
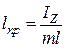 (11)
(11)
Следовательно, приведённая длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. Исходя из определения (11), период колебаний физического маятника можно записать:
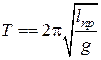 (12)
(12)
Точка «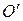 », лежащая на продолжении прямой
», лежащая на продолжении прямой 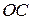 (Рис. 1.), отстоящая от точки подвеса на расстояние
(Рис. 1.), отстоящая от точки подвеса на расстояние 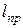 , называется центром качания физического маятника. Центр качания примечателен тем, что период физического маятника не изменяется, если точкой подвеса сделать точку «
, называется центром качания физического маятника. Центр качания примечателен тем, что период физического маятника не изменяется, если точкой подвеса сделать точку «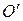 ». Применяя теорему Штейнера, получим:
». Применяя теорему Штейнера, получим:
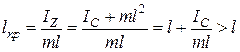
то есть 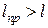 .
.
Измеряя значения периода 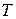 ,
, 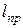 для физического маятника, из формулы (12) можно выразить ускорение свободного падения
для физического маятника, из формулы (12) можно выразить ускорение свободного падения 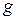 .
.
 2015-05-14
2015-05-14 285
285







