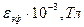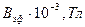Тарирование проводят в магнитном поле, величина которого известна.
В данной лабораторной работе используют магнитное поле длинного соленоида. Эффективное значение магнитного поля на оси соленоида рассчитывается по формуле
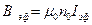 (5)
(5)
где n0 - число витков на единице длины обмотки соленоида; Iэф - эффективное значение тока обмотки соленоида.
При проведении тарирования измерительную катушку помещают в центре длинного соленоида так, чтобы угол между направлением вектора индукции В и нормалью к поперечному сечению катушки был равен 0 °. Затем измеряют максимальную величину эффективного значения ЭДС измерительной катушки εэфmax как функцию переменного тока, питающего длинный соленоид. После этого по формуле (3) рассчитывают значения Bэф, соответствующие значениям Iэф. Строят тарировочный график зависимости εэф max =f(Bэф). График представляет собой прямую, выходящую из начала координат. Коэффициент наклона этой прямой к оси абсцисс (угловой коэффициент k) равен
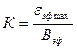 (6)
(6)
Ход работы:
Были проведены измерения ε[мВ] и рассчитаны по формуле (7)
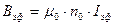 (7)
(7)
значения модуля магнитной индукции. Результаты измерений и расчетов представлены в таблицы 1.
Таблица 1
Результаты измерений ЭДС
| Iэф,A | εэф max, мВ | 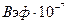 ,Тл ,Тл
| К’,В/Тл | Примечание | |
| εув, мВ | εум,мВ | εср,мВ | n0=830витков/м μ0=4π10-7Гн/м | ||
| 0,5 | 60,2 | 60,3 | 60,25 | 5212,4 | 9,98 |
| 122,3 | 122,4 | 122,35 | 10424,8 | ||
| 1,5 | 186,1 | 186,2 | 186,15 | 15637,2 | |
| 250,1 | 250,1 | 250,1 | 20849,6 |
По данным таблицы 1 был построен график зависимости эффективного значения ЭДС от эффективного значения модуля магнитной индукции, представленный на рис.1.
|
|
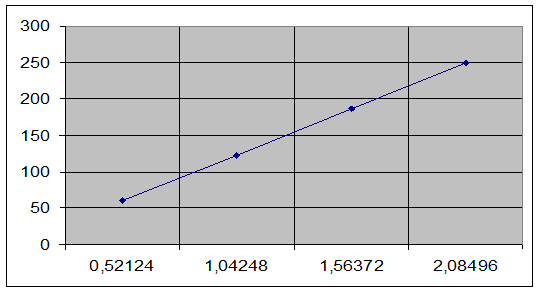
Для нахождения углового коэффициента К, выразим его из формулы метода наименьших квадратов:
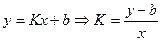
Для этого найдем b по формуле:
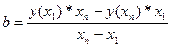 =
= 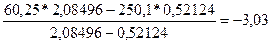
К= 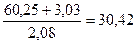
Затем по формуле (8):
К’=1,025К (8)
определили значение реального углового коэффициента К’=31,18.
Затем произвели ряд измерений ε[мВ] для точек, указанных в таблице 2. Рассчитали экспериментальные и теоретические значения модуля магнитной индукции. Результаты представлены в таблице 2.
Таблица 2
Результаты измерений ЭДС и расчетов амплитудной индукции
| Местоположение точки | ε,мВ | Вэксп,мТл | Втеор, мТл | Примечание |
| В центре на оси короткого соленоида | 184,7 | 74,02806 | 1,99 | μ0=4π10-7Гн/м R=0,1м N=212витков I=1,5A |
| В центре на расстоянии равном радиусу короткого соленоида | 61,5 | 24,6493 | ||
| В центре на большом расстоянии от короткого соленоида | 5,3 | 2,124248 | ||
| Вдоль линии, перпендикулярной оси короткого соленоида в девяти точках: | ||||
| 184,8 | 74,06814 | |||
| 75,7515 | ||||
| 194,3 | 77,87575 | |||
| 207,1 | 83,00601 | |||
| 184,5 | 73,9479 | |||
| 188,5 | 75,5511 | |||
| 198,4 | 79,51904 | |||
| 207,7 | 83,24649 | |||
| 182,4 | 73,10621 | |||
| Во всех точках, находящихся между двух коротких соленоидов: | ||||
| 181,8 | 72,86573 | |||
| 177,3 | 71,06212 | |||
| 176,3 | 70,66132 | |||
| 177,4 | 71,1022 | |||
| 180,9 | 72,50501 | |||
| 170,2 | 68,21643 | |||
| 168,1 | 67,37475 | |||
| 166,4 | 66,69339 | |||
| 167,7 | 67,21443 | |||
| 169,2 | 67,81563 | |||
| 157,7 | 63,20641 | |||
| 151,2 | 60,6012 | |||
| 61,72345 | ||||
| 154,9 | 62,08417 | |||
| 138,3 | 55,43086 | |||
| 138,5 | 55,51102 | |||
| 136,8 | 54,82966 | |||
| 138,5 | 55,51102 | |||
| 139,7 | 55,99198 | |||
| 122,2 | 48,97796 | |||
| 122,9 | 49,25852 | |||
| 121,3 | 48,61723 | |||
| 49,2986 | ||||
| 122,8 | 49,21844 | |||
| 105,5 | 42,28457 | |||
| 106,4 | 42,64529 | |||
| 104,7 | 41,96393 | |||
| 105,2 | 42,16433 | |||
| 104,6 | 41,92385 | |||
| 36,07214 | ||||
| 91,9 | 36,83367 | |||
| 91,5 | 36,67335 | |||
| 91,3 | 36,59319 | |||
| 90,2 | 36,1523 | |||
| 76,7 | 30,74148 | |||
| 31,66333 | ||||
| 77,7 | 31,14228 | |||
| 79,3 | 31,78357 | |||
| 77,4 | 31,02204 | |||
| 26,85371 | ||||
| 67,5 | 27,05411 | |||
| 66,6 | 26,69339 | |||
| 66,8 | 26,77355 | |||
| 66,5 | 26,65331 | |||
| 54,9 | 22,00401 | |||
| 54,3 | 21,76353 | |||
| 56,9 | 22,80561 | |||
| 22,84569 | ||||
| 56,7 | 22,72545 | |||
| 48,4 | 19,3988 | |||
| 48,1 | 19,27856 | |||
| 47,6 | 19,07816 | |||
| 48,1 | 19,27856 | |||
| 48,8 | 19,55912 | |||
| 41,5 | 16,63327 | |||
| 17,23447 | ||||
| 16,83367 | ||||
| 42,3 | 16,95391 | |||
| 41,2 | 16,51303 |
Вывод: В ходе работы были измерены значения ЭДС: в длинном соленоиде при различных значениях силы тока; в центре короткого соленоида и на различных расстояниях от него при постоянном значении силы тока I=1,5A; между двумя короткими соленоидами. Для полученных значений ЭДС рассчитали модуль магнитной индукции. Экспериментальные данные не совпали с теоретическими.
 2015-05-14
2015-05-14 641
641