2015-05-14
458
Рассмотрим результирующее колебание в т. М, возникающее при сложении двух гармонических колебаний из т.т. О1 и О2, например с начальными фазами равными нулю и одинаковыми амплитудами:
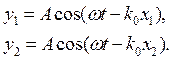
Здесь А - амплитуда волны;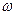 
- циклическая частота волны;
t - время; k0 =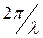 
- волновое число; 
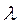- длина волны.
Y
 |
M
o
X
 |
Y- смещение колеблющейся точки среды
Рисунок 4 - Схема распространения бегущей поперечной волны
O1 x1 M
 |
x2
O2
О1, О2 - источники волн; х1, х2 - расстояния до исследуемой т. М
Рисунок 5 - Схема наложения двух когерентных волн в т. М.
Результирующее смещение т. М будет зависеть от координат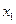 
и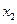 
.
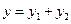
Далее по формуле суммы косинусов:
,
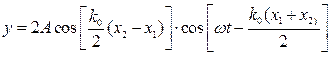где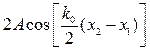 
- амплитуда результирующего колебания, не зависящая от времени и меняющаяся от точки к точке.
1. Рассмотрим условия, когда амплитуда результирующего колебания достигает максимума. Интерференционный максимум наблюдается, когда на разности хода волн укладывается четное число полуволн:
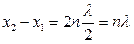, (32)
где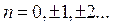 
Во всех точках пространства, для которых выполняется условие (32),будет наблюдаться интерференционный максимум:
.
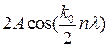Учитывая, что волновое число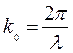 
, получим 
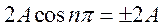- максимальная амплитуда.
2. Если на разности хода волн укладывается нечетное число полуволн
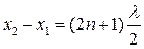, (33)
то в таких точках пространства амплитуда результирующих колебаний будет иметь минимальное значение:
.
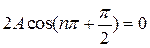Волны как бы гасят друг друга, поэтому условие (33) называется условием интерференционного минимума.
