По альтернативному признаку

При выборочном контроле по результатам проверки выборки обычно принимают одно из следующих решений:

1. Принять непроконтролированную (оставшуюся) часть партии без дальнейшего контроля.

2. Отвергнуть оставшуюся часть партии без дальнейшего контроля.

3. Провести сплошной контроль оставшейся части партии.

Например, в случае одноступенчатого контроля возможные типы планов можно обозначить так: (nc)₁₂, (nc)₁₃, (nc)₂₃. Если, допустим, при плане (nc)₁₂ окажется, что в выборке m  c, принимается решение 1. Если же m>c, принимается решение 2. Ранее рассматривались именно планы типа (nc)₁₂.

Рассмотрим план (nc)₁₃, когда отклонённые партии подвергаются сплошному контролю, т.е. контролируются оставшиеся (N-n) изделий, а выявленные дефектные изделия заменяют годными. Пусть на контроль поступают партии изделий с постоянным уровнем дефектности q. Тогда партии принимаются с вероятностью P(q), и уровень дефектности в принятых партиях равен 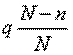. Партии отклоняются и подвергаются сплошному контролю с вероятностью 1 – P(q). Уровень дефектности в этих партиях равен 0. Тогда средний выходной уровень дефектности AOQ равен

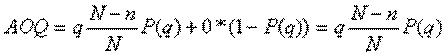
Поскольку AOQ = 0 при q = 0 и при q = 1, то внутри интервала 0  q  1 имеется некоторое максимальное значение AOQ. Этот максимальный для заданного плана контроля средний уровень дефектности называют пределом среднего выходного уровня дефектности AOQL.

При использовании плана (nc)₁₃ число проконтролированных в партии изделий есть случайная величина, принимающая значение n с вероятностью P(q), и значение N с вероятностью 1-P(q). Поэтому среднее число проконтролированных изделий в партии

n_ср= n*P(q) + N*(1-P(q))

При налаженном производстве партий одинакового объёма N количество дефектных изделий в i-й партии D_i является случайной величиной. Последовательность чисел D_i имеет интегральную функцию распределения

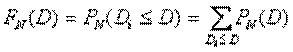
Для получения оценок распределения F_N(D), а также среднего входного уровня дефектности qср, обычно используют информацию, накапливаемую в процессе проведения контроля, а на начальных этапах организации контроля с этой целью проводят сплошной контроль определённого числа партий.

Пример 11.1. Сплошному контролю подвергнуто k = 100 партий по N = 250 изделий в каждой. Результаты контроля приведены в табл. 11.1, в которой m_D означает число партий с D дефектными изделиями. Требуется получить оценку среднего входного уровня дефектности, а также проверить гипотезу, что число дефектных изделий в партии D подчиняется распределению Пуассона.

Таблица 11.1.

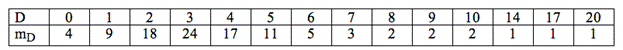
В ячейку А1 новой книги Excel вводим заголовок работы. В ячейки В3 и В4 вводим соответственно объём партии и количество партий. В диапазон А7:В20 вводим данные табл. 11.1 с заголовками столбцов D и m_D в ячейках А6 и В6.

Оценку среднего входного уровня дефектности можно получить как отношение общего числа дефектных изделий во всех проконтролированных партиях к общему числу изделий, т.е.

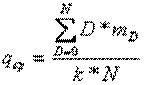
Для нахождения qср вводим столбец с заголовком D*m_D с заголовком в ячейке С6. Соответствующие произведения рассчитываем в диапазоне С7:С20. В ячейке Е3 рассчитываем значение qср. Для этого находим сумму ячеек С7:С20 с помощью математической формулы СУММ, затем переводим курсор в строку формул и делим полученную сумму на N и k. Формула в ячейке Е3 будет выглядеть, например, так: =СУММ(C7:C20)/B4/B3. В результате получим значение qср, равное 0,01584.

Поскольку qср < 0,1, то можно предположить, что число дефектных изделий в партиях D действительно распределено по закону Пуассона. Для проверки этого воспользуемся критерием согласия Пирсона.

Вначале необходимо рассчитать теоретическую частоту m_D теор появления партий с D дефектными изделиями. Она равна

m_D теор= k*P(D),

где P(D) – вероятность появления партии с D дефектными изделиями. Как мы предположили, P(D) должно описываться дифференциальной функцией распределения Пуассона, рассчитываемой по статистической формуле ПУАССОН. Таким образом, вводим столбец с заголовком m_D теор в ячейке D6, и в ячейке D7 рассчитываем значение m_D теор для D = 0. Поскольку m_D теор должно быть целым числом (теоретическое число партий с D дефектными изделиями), то в ячейку D7 вначале вводим математическую формулу ОКРУГЛ (округляет число до указанного количества десятичных разрядов). Во вторую строку открывшегося диалогового окна вводим 0 как количество десятичных разрядов, до которого нужно округлить. В первую строку вводим округляемое число, в данном случае - произведение k*P(D). В качестве k вводим ссылку на ячейку В4, затем вводим знак *. Далее в качестве выражения для P(D) встраиваем функцию ПУАССОН. Для этого в строке формул открываем список функций, выбираем Другие функции… и открываем функцию ПУАССОН. Учитывая, что каждая партия представляет собой выборку из общего потока продукции, в первую строку диалогового окна функции ПУАССОН вводим количество дефектных изделий в партии, т.е. ссылку на ячейку А7. Во вторую строку вводим значение математического ожидания числа дефектных изделий в партии, равное произведению N*qср, т.е. буквально выражение B3*E3. В третью строку вводим значение ложь, поскольку P(D) представляет собой дифференциальную функцию распределения Пуассона. В результате в ячейке D7 получаем значение 2. Формула в ячейке D7 выглядит так: =ОКРУГЛ(B4*ПУАССОН(A7;B3*E3;ЛОЖЬ);0). После указания необходимой абсолютной адресации формулу из D7 копируем в диапазон D8:D20.

Перед расчётом наблюдаемого значения критерия Пирсона рекомендуется просуммировать с соседними те частоты появления партий m_d (и m_D теор соответственно), которые имеют значения меньше 5. Новые значения m_d и m_D теор вводим с клавиатуры в диапазон F7:G13.

Наблюдаемое значение критерия Пирсона рассчитываем по формуле

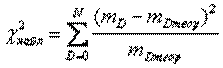
Для этого сначала в диапазоне Н7:Н13 рассчитываем значения

Затем в ячейке Н3 рассчитываем наблюдаемое значение критерия Пирсона. Расчётная формула выглядит так: =СУММ(H7:H13). Получаем значение 6,716666667.

В ячейке Н4 находим табличное значение критерия Пирсона 2таблпо статистической формуле ХИ2ОБР (находим именно обратное значение распределения хи-квадрат, т.к. ищется квантиль от функции распределения, а не наоборот). В диалоговом окне функции в строку Вероятность вводим значение уровня значимости 0,05. В строку Степени_свободы вводим число степеней свободы, равное l – c – 1, где l – количество интервалов, т.е. количество значений m_D, равное 7; с – количество параметров распределения, равное 1 (параметр ). Таким образом, число степеней свободы равно 5. Рассчитанное табличное значение критерия Пирсона равно 11,07048257. Поскольку 2табл > 2набл, то гипотеза о виде распределения не отвергается. Примем. что распределение числа дефектных изделий в партиях подчиняется закону Пуассона. Результаты расчётов показаны на рис. 11.1.