Түрлі жиілікті диапазондардағы радиобайланыс арналары көптеген жағдайларда аралық станцияларсыз алшақтатылған байланысты ұйымдастыруға мүмкіндік береді, сондықтан кабельдімен салыстырғанда неғұрлым үнемді болып табылады.
Көп арналы телефонды және теледидарлық байланыста ондаған мегагерцтен ондаған гигагерцке дейін жиілікті диапазонда жұмыс істейтін жердегі радиорелейлі байланыс арналары кең таралды дейге болады.
Спутникті байланыс желілері қызмет атқару қағидасы бойынша жасанды Жер серіктерінде орнатылған ретрансляторлары бар радиорелейлі желілердің көп түрлілігін білдіреді, ол әрбір серік үшін 10000 км шамада байланыс алшақтығын қамтамасыз етеді. Спутниктік байланыс жиілігінің диапазоны қазіргі таңда 250 ГГц-ке дейін кеңейтілген, ол байланыс жүйелерінің сапалы көрсеткіштерінің артуын қамтамасыз етеді.
Неғұрлым жоғары жиілікті диапазондарға өту антенналардың шағын көлемі барысында тік бағытталған сәулені алуға мүмкіндік береді, атмосфералық және өнеркәсіптік тосқауылдар ықпалын азайтуға, кең сызықты байланыс арналарын ұйымдастыруға мүмкіндік береді.
Арналардың енуі және шығауындағы сигналдардың сипаты бойынша дискретті, үздіксіз және дискретті-үздіксіз арналарды бөліп қарастыруға болады.
C арнасының өткізу қабілеттігі төмендегідей анықталады
C = V max H, (1)
мұндағы V – электрлі кодты сигналдарды беру жылдамдығы, H – хабарлама энтропиясы.
Арнаны пайдалану коэффициенті
η= V / C, 0≤η≤1, (2)
себебі 0≤V≤C.
Әмбебап дискретті арналар
Кодер берілетін символдардың электрлі кодты сигналдарға өзгертілуін қамтамасыз етеді. Әмбебап арнада енгізу мен шығаруда кодты сигналдар элементтері арасында бір текті сәйкестік болады (арнада қателіктер болмайды). Ақпаратты беру жылдамдығы кодердің өнімділігіне тең
C k= V k H k [бит/с], (3)
мұндағы V k=1/ L – элементті кодты сигналдарды беру жылдамдығы [сигн./с], Hk – кодер энтропиясы [бит/сигн.], L – элементті кодты сигнал ұзақтығы.
Әмбебап арнаның өткізу қабілеттігі
C = V max= V klog m k, (4)
мұндағы m k – кодтың негіздемесі. Өткізу қабілеттігі арнаның шекті сипаттамасы болып табылады. Егер код негіздемесі mk тең болып, бір элементті код сигналын беру үшін L уақыты қажет болса, онда n ұзындықты сигналдардың кодты жиынын беру үшін T = nL уақыты қажет болады. T ұзақтықты кодты жиындардың жалпы саны N (T) = mkn тең. Сәйкесінше, бір кодты жиындағы ақпараттың максималды саны H max= n log m k. Өткізу қабілеттігі мынаған тең
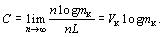 (5)
(5)
Осылайша, әмбебап дискретті арнаның өткізу қабілеттігін сигналдарды беру жылдамдығы мен код негіздемесі толығымен анықтайды.
Әмбебап дискретті арна үшін Шеннон теоремасы (дәлелдеусіз): егер дискретті арнада қателіктер болмаса, онда V орташа жылдамдығымен ақпаратты беру үшін қайнар көздің шығу жолында хабарламаны кодтауға болады. V > C-ден ақпаратты беру мүмкін емес.
Бұл теорема оптималды тиімді кодтарды құру үшін теориялық негіз болып табылады. Егер кодердің шығу жолындағы кодтау процесінде тең ықтималды тәуелсіз кодты сигналдардың пайда болуын қамтамасыз ететін болсақ, онда әрбір элементті сигнал максималды ақпарат көлеміне ие болып, кодердің өнімділігі максималды болады, ал ақпаратты беру жылдамдығы арнаның өткізу қабілетіне жақындайды.
Нақты дискретті арналар
Нақты арналарда үнемі хабарлааларды беру барысында қателіктер болады. Қателіктер арнаның өткізу қабілеттігінің жоғалуы мен ақпараттың жоғалуына әкеледі. Қателіктердің пайда болу ықтималдығы көбінесе сигналдардың бұзылуы мен тосқауылдардың пайда болуымен анықталады.
Берілген символға қатысты қабылданған символ қамтитын ақпарат көлемін немесе өзге символға қатысты бір символдың қамтитын ақпарат көлемін символдардың бірлемкен пайда болу ықтималдығы үшін келесі формула көмегімен табады
P (a i, a j’) = P (a i) P (a j’/ a i) = P (a j’) P (a i/ a j’), (6)
мұндағы P (a i) и P (a j’) – a i және a j’ символдарының пайда болу ықтималдығы, P (a i/ a j’) – шартты ықтималдық.
Қабылданған кодты сигналды a k2, ал берілген кодты сигналды a i1 деп белгілейік. Берілген a i1 –ге қатысты a k2 қабылданған символ қамтитын ақпарат көлемі былайша анықталады:
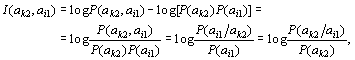 (7)
(7)
мұндағы P(a k2, a i1) – a k2, a i1 символдарының бірлескен пайда болу ықтималдығы; P (a i1), P (a k2,) – a k2, a i1 пайда болу ықтималдығы; 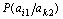 ,
, 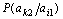 – сәйкес шартты ықтималдықтар. Егер символдар тәуелсіз пайда болса, онда
– сәйкес шартты ықтималдықтар. Егер символдар тәуелсіз пайда болса, онда 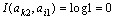 . Барлық қалған жағдайларда бір символ өзге символ туралы ақпаратты қамтиды және
. Барлық қалған жағдайларда бір символ өзге символ туралы ақпаратты қамтиды және 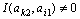 .
.
Бір символ әкелетін қабылданған ақпараттың орташа көлемін (7) формуласын барлық i және k бөле отырып, аламыз, ал дәлірек айтсақ
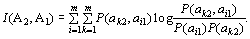 (8)
(8)
(7) бөлшегінің екі формасын ескере отырып, ақпарат көлемі үшін екі жазу бөлшегін аламыз:
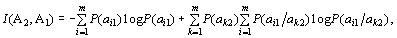 (9)
(9)
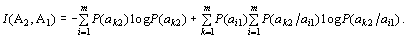 (10)
(10)
(9) және (10) формулаларын төмендегідей көрнекі түрде бейнелеуге болады:
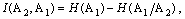 (11)
(11)
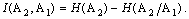 (12)
(12)
(11), (12) формулаларының мағынасы мынадай. H (A1) шамасы – бұл кодер энтропиясы, ал Н(A1/A2) шамасы – бұл арнада қателіктер үшін жоғалтылған ақпараттың орташа көлемі. Сәйкесінше, (11) ара-қатынасы бір символда қабылданған ақпараттың орташа көлемін қабылданған символ энтропиясы мен тосқауылдар айырмасы ретінде анықтауға болатынын көрсетеді. (12) ара-қатынасын жиірек қолданады, себебі ол анықтауға жеңіл болатын тосқауыл энтропиясы арқылы 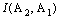 анықтауға мүмкіндік береді.
анықтауға мүмкіндік береді.
Нақты арналардағы ақпаратты беру жылдамдығы 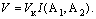 тең. Екі соңғы формулаларды пайдалана отырып, келесіні аламыз:
тең. Екі соңғы формулаларды пайдалана отырып, келесіні аламыз:
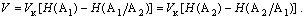 (13)
(13)
Егер қателіктер болмаса, онда 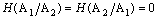 және (13) формуласы әмбебап арна үшін арналған формулаға айналады, онда
және (13) формуласы әмбебап арна үшін арналған формулаға айналады, онда 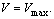
Нақты дискретті арналардың өткізу қабілеттігі мынаған тең:
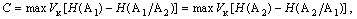 (14)
(14)
Мұнда максимумды іздеу операциясы сигналдарды беру және өңдеудің барлық тәсілдері бойынша орындалады.
Нақты дискретті арналар үшін Шеннон теоремасы мынадай (дәлелдеусіз): егер хабарлама қайнар көзі өнімділігі арнаның өткізу қабілеттігіне қарағанда төменірек болса, онда хабарламаны дискретті арна бойынша төмен қателіктер ықтималдығымен ақпаратты беретіндей кодтауға болады.
Аталмыш теорема түзетуші кодтаудың теориялық негізі болып табылады..
Есептер:
1. X үшін Хаффмен кодының блокты коды үшін 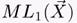 есептеу. Блок ұзындығы
есептеу. Блок ұзындығы
— 2 бит. X -ғы дискретті сигнал соңғы мысалдан алынады.
2. X үшін Хаффмен және Шеннон-Фэно кодтары үшін НX және ML(X] есептеу.
X –гі дискретті сигнал ықтималдықтарды келесідей бөлу арқылы беріледі:
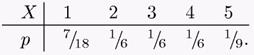
3. Д.С.-дан әрбір сигнал мағынасы туралы шағымдалған хабарлама бірлігіне қатысты биттің орташа көлемін есептеу. Ол үшін Шеннон-Фэно, Хаффмен және арифметикалық тәсілмен ықтималдықтардың келесідей бөлінуі берілген.  .
.
4. Шеннон-Фано кодымен 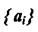 ансамблін кодтау, егер символдар ықтималдығы төменде келтірілген мәндерге тең болса.
ансамблін кодтау, егер символдар ықтималдығы төменде келтірілген мәндерге тең болса.
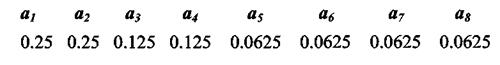
Кодты жиын символдарының орташа санын табу. Кодтың артық қалуын анықтау.
Тақырып 10. Физикалық деңгейде ақпараттық процестер.
Мақсаты: модуляция әдісін қарастыру және сандық модуляция әдісіне салыстырмалы сипаттама жүргізу.
Жоспар (1 сағат)
1. Модуляция және демодуляция процедураларының мәні және мазмұны.
2. Модуляцияның әртүрінің кедергі тұрақтылығы бойынша салыстырмалы сипаттама.
3. Модуляцияның сандық әдісі.
Кілттік сөздер: модуляция, демодуляция,Шеннон, фильтр, әдістер.
Хабарламалар сигналдар көмегімен беріледі. Қарапайым жағдайда хабарлама қабылданған сигналдың болуымен (болмауы) сипатталауы мүмкін. Мұнда сигналды анықтау мәселелін шешу қажет. Көптеген жағдайларда берілетін сигналдар түрі алдын-ала белгілі болады, және хабарламаның қабылдануы мүмкін болатын сигналдардың қайсысы берілгендігін анықтаудан тұрады. Онда мәселе сигналдарды айыра білуден тұрады. Егер сигналдар қандай да бір интервал аралығында тұрақты болып табылатын параметрлер мәндерімен ерекшеленетін болса, онда сигналдың параметрлерін бағалау қажет. Хабарлама параметрлер өзгерістерінде қамтылуы мүмкін, яғни олардың сәттік (локальды) мәндерінде. Онда хабарламаны алу үшін сигналдың параметрлерін фильтрлеуді жүзеге асыру қажет. Фильтрлеу мәселесі, тәртіп бойынша, параметрлерді бағалауға қарағанда неғұрлым күрделі болып табылады.
Берілетін хабарламаларға сәйкес ақпараттық параметрді басқару модульдеу деп аталады.
Ақпараттық сигналды (хабарлама) - θ(x), хабарламаға сәйкес параметрі өзгеретін тасымалдаушы-сигнал - s(x). Модульдеу барысында осы екі сигнал төмендегі теңгеуге сәйкес ξ (x) бір модульденген сигналға өзгереді
ξ(x)=M{ s (x),θ(x)}, (1)
мұндағы М{.} – модульдеу түрімен анықталатын оператор. θ(x) хабарламасын қабылдау жағында белгілеу үшін кері қайта құруды жүзеге асыру қажет (демодульдеу), яғни
θ(x)=M-1{ξ(x)}. (2)
s (x) тасымалдау-сигнал мен θ(x) ақпараттық сигналдың түріне, функционалды формасы мен параметрлер санына байланысты модульдеудің түрлі әдістерінің қасиеттері өзгереді, ал дәлірек айтсақ, ξ(x) сигнал спектрінің түрі мен ені, тосқауылдар ықпалына төзімді болуы.
Егер тасымалдау-сигналдың ақпараттық параметрі үздіксіз өзгеретін болса, онда модульдеу әдістері үздіксіз болып табылады мысалы, амплитудалық, фазалық, жиілікті үздіксіз модульдеу әдістері кең таралған).
Тасымалдаушы-сигнал ретінде импульстардың кезеңдік ілеспелілігін жиі қолданады, онда модульдеуді импульсті деп атайды (мысалы, θ(x) заңы бойынша амплитуда мен импульстар жиілігінің өзгеруі барысында амплитудалы-импульсті немесе жиілікті-импульсті модульдеу орын алады.
Ақпараттық параметр мәндердің сандық көлеміне ие болуы мүмкін, мұнда модульдеуді дискретті деп атайды. Модульдеудің дискретті түрлірені, мысалы, амплитудалық, жиілікті және фазалық манипуляцияны жатқызуға болады. Егер параметр мәндері кодталған болса, және сандық формада берілсе, онда модульдеудің сәйкес түрлері сандық модульдеу атауына ие болады. Сандық модульдеудің неғұрлым кең таралған түріне импульсті – кодты модульдеуді жатқызуға болады, онда дискретті нүктелердегі сигнал мәндерін сандық формада кодтайды.
Сигналдарды беру жүйесін құру барысындағы негізгі мәселе – жоғары жылдамдық, шынайылық және ақпаратты беру барысындағы тосқауылдардан қорғанушылық тарапынан модульдеу-демодульдеудің оптималды режимдерін анықтайтын әдістер мен математикалық модельдерді өңдеу.
Модульдеу түрлерін жіктеу барысында сигнал мен тасымалдаушы-сигнал түрін, сипатын ескереді: детерминацияланған процесс, кездейсоқ стационарлы процесс, стационарлы емес процесс және т.б. Детерминацияланған сигналдар Фурье қатарларының қасиеттері мен Фурье қайта құрулары негізінде олардың амплитудалық және фазалық спектрлерімен анықталады. Сигналдар ақпараты мен оларды беру теорияларында стохастикалық сигналдар ерекше орынға ие. Олар корреляциялық функциялар мен спектрлі тығыздықтар сияқты берілген сипаттамалары бар кездейсоқ процестердің жүзеге асырулары болып табылады.
Егер ақпараттық сигнал, тасымалдаушы-сигнал түрлері және жері сипаттамалары алдын-ала берілген болса, онда негізгі мәселе сигралдарды тиімді қабылдау болып табылады. Тиімді қабылдау мәселесі, тәртіп бойынша, тосқауылдар жағдайында берілген критерий бойынша сигналдарды айыра білуден тұрады.
Хабарламаларды қабылдау мәселелерін екі класқа жіктейді –когерентті және когерентті емес қабылдау, сәйкесінше ақпаратты беру арнасында синхронизацияның болуы немесе болмауы барысында. Когерентті қабылдау әдістері (синхронды), тәртіп бойынша, неғұрлым қарапайым және сенімді. Когерентті емес (асинхронды) қабылдау тәсілдері неғұрлым жоғары ықпал етуді қамтамасыз етеді, алайда жүзеге асыру барысында неғұрлым күрделі.
Амплитудалық, фазалық және жиілікті модульдеу әдістері
Гармониялық тасымалдаушы-сигналдардың амплитудалық, фазалық және жиілікті модульдері радиохабарлау мен бпйланыс жүйелерінде неғұрлым кең таралды.
Амплитудалық модульдеу
Амплитудалы-модульденген (АМ) сигнал жалпы жағдайда төмендегі формуламен анықталады
ξ(x)=[1+ m θ(x)] s (x), (3)
мұндағы Q(x) – ақпараттық (модульдейтін) сигнал, s (x)– тасымалдаушы-сигнал, m – модульдеу коэффициенті.
Сигнал спектрін (3) Фурье қайта құруын төмендегі формада қолдану арқылы табуға болады (2.5 тарау):
X(u)=F{x(x)}= S (u)+m S (u)*Q(u), (4)
мұндағы S(u)=F{s(x)}, Q(u)=F{θ(x)}.
Спектрдің құрылуы (4) 3.1 және 3.2 суреттерінде сипатталған.
Гармониялық модульдеуші сигналда (сурет 3.1) оның спектрі, тасымалдаушы-сигналдағы спектрі сияқты екі дельта-функцияларды білдіреді. S(u) және Q(u) спектрлерінің үйлесуі Q(u) спектрін ± u 0 неғұрлым жоғары жиілігіне ауысуына әкеледі.
Егер модульдеуші сигнал күрделі формаға ие, сәйкесінше, жиілікті осьтің түрлі жағдайлары бар көптеген дельта-функциялар жұптарының көмегімен құрылған созылмалы спектрге ие болса (сурет 3.2), онда спектрді неғұрлым жоғары жиілікке ± u 0 аусуы барысында сәйкес спектрлі тәртіптер құрылады. Фурье қайта құрулары жиілікті симметриялы қасиеттерінің күшіне байланысты барлық пайдалы ақпарат ± u 0 жиілік шеңберіндегі спектрлі тәртіпте болатынын көрсетуге болады.
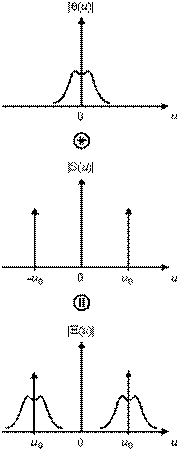
АМ сигналының демодульдеуін детектордың шығу жолында төменг жиіліктер фильтрленуі барысында тасымалдаушы-сигналды бөліп көрсету жолымен жүзеге асырад. Фильтрді өткізу сызығының ені сигналдың қалпына келуі барысындағы минималды спектрлі бұзылуларды қамтамасыз ету үшін Q(u) спектрінің еніне сәйкес келуі керек (сурет 3.2).
Фазалық модульдеу
Фазомодульденген (ФМ) сигнал тұрақты амплитудаға ие, сигнал фазасы ақпараттық сигналға пропорционалды түрде өзгереді, ал дәлірек айтсақ:
ξ(x)= A cos[2π u 0 x +mθ(x)], (5)
мұндағы ± u 0 - тасымалдаушы жиілік, m – фазалық модульдеу индексі.
Модульдеуші сигнал гармониялық болып табылсын, θ(x)=cos(2π u m x), және модульдеу индексі m<<1. Мұнда (5) формуласын былайша қайта жазуға болады:
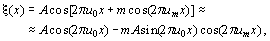 (6)
(6)
Онда мынаны ескеру қажет 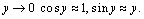 Екінші бөліндінің қайта құрылғанынан кейін (6) мынаны аламыз
Екінші бөліндінің қайта құрылғанынан кейін (6) мынаны аламыз
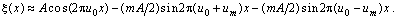 (7)
(7)
Шағын модульдеу индексі бар ФМ-сигнал спектрі 19.3.суретінде көрсетілген.
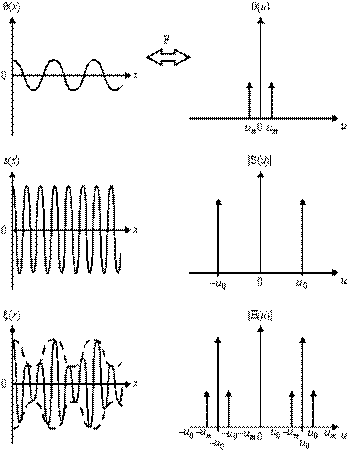
Сурет 19.1. Күрделі гармониялық
модульденуі бар АМ сигналының спектрі
Сурет 19.2. АМ сигналының спектрі
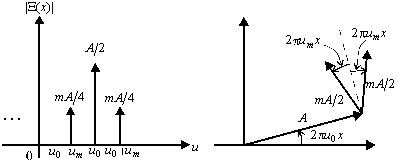
Сурет 19.3. m <<1  барысында ФМ сигналы үшін спектр мен векторлы диаграмма
барысында ФМ сигналы үшін спектр мен векторлы диаграмма
Спектрлі құраушылар шамалары синусоидалды АМ сигналының спектрлі құраушылары шамаларына тең, алайда тасымалдаушы мен бүйірлі құраушыла арасындағы фазалық ара-қатынас түрліше болады. Осы фазалық ара-қатынастар 3.3 суретінің оң жақ бөлігіндегі векторлы диаграммада неғұрлым толық көрсетілген. Аз ғана векторлар айналатын үлкен вектор бойымен жылдам қарама-қайшылықта бәсең түрде өзгереді, ал ζ(x) горизонталды оське векторлар сомасының проекциясын білдіреді. Алайда АМ сигналы жағдайына қарағанда шағын векторлар сомасы үнемі үлкен векторға перпендикулярлы болып табылады. Мұнда, егер бүйірлі құраушылар векторлары (m << 1) төмен болса, онда сомалық вектор ұзындығы шамасы бойынша A тасымалдаушы амплитудасына жақын болады, бірақ нәтижелеуші вектор ауыспалы жылдамдықпен айналады.
Аталмыш векторлы ара-қатынастағы фазалық ара-қатынастар q(x) туынды модульдеуші сигналы барысында шағын индексті модульдеуі бар (сурет 3.4) ФМ сигналдарды генерациялаудың қарапайым тәсілін көрсетеді.
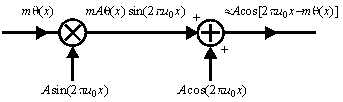
Сурет 19.4. m <<1 барысындағы модульдеушінің ФМ құрылымдық сызбасы
Жиілікті модульдеу
Жиілікті модульдеу барысында q(x) ақпараттық сигналына сәйкес s (x) тасымалдаушы-сигналдың u (x) сәттік жиілігі өзгереді, дәлірек айтсақ
θ(x)=Acos[2π u (x) x ], (8)
мұндағы
u (x)= u 0+ 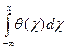 . (9)
. (9)
Синусоидалды ЧМ барысында модульдекші сигнал мынадай түрге ие болады:
θ(x)=- a sin(2π umx), (10)
онда
u (x)= u 0+ 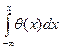 = u 0+(a /2π um)cos(2π umx). (11)
= u 0+(a /2π um)cos(2π umx). (11)
(11)-мен ескере отырып, (6) және (8) салыстыра отырып синусоидалды модульдеуші функция мен |m|= a /2π u m модульдеу индексі барысында ФМ және ЧМ біртектілігін көрсетеді.
a мәні 2π u 0 тасымалдаушы бұрыштық жиілігіне қатысты сәттік бұрыштық жиіліктің максималды девиациясын білдіреді.
ЧМ сигналдар үшін қарапайым демодулятор немесе жиілікті дискриминатор резонансты контурды білдіреді, мысалы тасымалдаушы жиіліктен төмен орнатылған (сурет 3.5). Енгізуші модульденген сигналдағы сәттік жиіліктің өзгеруі резонансты контурдың шығу жолында сигнал амплитудасының өзгерістеріне ауысады. Аталмыш амплитудалық өзгерістерді әдеттегі детектор көмегімен бөліп көрсету қиын емес.
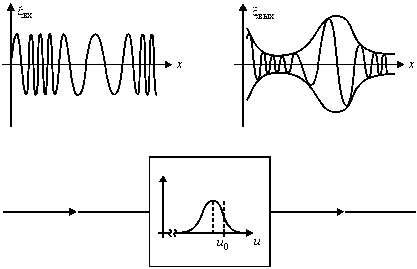
Сурет 19.5. Жиілік өзгерісінің резонансты тізбек көмегімен амплитуда өзгерісіне ауысуы
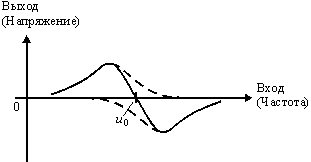
Сурет 19.6. Резонансты контурлар жұбының көмегімен алынған дискриминатор сипаттамалары
Осындай дискриминатордың шектеулі диапазонының сызықтықтарын контурлар жұбын қолдана отырып, кеңейтуге болады, олардың бірі сәйкесінше жоғарыға бағдарланған, ал екіншісі тасымалдаушы жиіліктен төмен орналастырылған. Осы контурлардың шығу жолындағы шығару сигналдары бөлек детектрленеді және содан кейін 3.6. суретінде көрсетілгендей, дискриминаторлардың толық сипаттамасын құрай отырып, шығады. Осындай типтегі дискриминаторлардағы шығарушы сигнал жиіліктер, сондай-ақ шығарушы сигнал амплитудасы вариациялары бойынша өзгереді.
Нақты жүйелерде ЧМ-сигналдағы бақыланбайтын амплитуда өзгерістері шулар, тосқауылдар нәтижесінде туындайды. Осыған байланысты дискриминаторлардың шығу жолында шектеушіні қосқан жөн, ол 3.7. суретінде көрсетілгендей сипаттамасы бар сызықтық емес құрылғыны білдіреді. Шектеуші оған шығу жолында қосылған резонансты күшейткішпен бірлесе отырып, фазалық өзгерістерді сақтай отырып, тар сызықты сигналдың амплитудалық өзгерісін жояды.
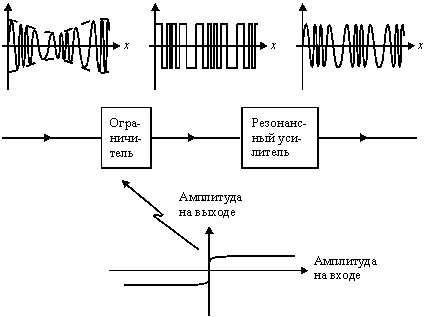
Сурет 19.7. Шектеуші мен резонансты күшейткіштің бірлескен жұмысы
3.8 суретінде типтік ЧМ қабылдаушының толық құрылымы көрсетілген.
Жоғары жиілікті күшейткіш (ЖЖК) қабылданған сигналды күшейтеді, ішкі гетеродин (генератор) гармониялық “жақтаушы” сигналды өңдейді. Нәтижесінде аралық жиіліктегі сигнал қалыптасады, ол ЖЖК мен гетеродин жиіліктерінің синхронды түзетілуі барысындатұрақты болып табылады.
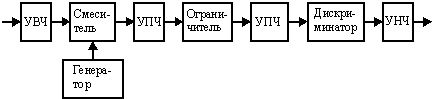
Сурет 19.8. ЧМ қабылдаушының функционалды сызбасы
Аралық жиілік күшейткіші (АЖК) сигнал күшеюінің жоғары коээфициентін қамтамасыз етеді. Күшейтілген сигнал шектеушіден кейін 3.7. суретте көрсетілген сызбадағыдай резонансты күшейткіш қызметін атқаратын екінші АЖК-ға келіп түседі. Жиілікті дискриминатор сигнал жиілігінің өзгерістерін бөліп көрсетеді, олар төменгі жиілікті сигнал формасында төменгі жиілікті күшейткіштің (ТЖК) кіріс жағына келіп түседі.
 2015-05-14
2015-05-14 1806
1806








