Шымкент-2011
УДК 681.3.7
Құрастырғандар: Құрақбаев Ж.С. «Тиімділеу әдістері» пәні бойынша лекция жинағы. – Шымкент, М.Әуезов атындағы ОҚМУ, 2011.- 56 б.
Әдістемелік нұсқау оқу жоспарының талаптарына және «Тиімділеу әдістері» пәнінің бағдарламасына сай жаслынып, курстың лекция жинағы. Әдістемелік нұсқау 5В060200 – «Информатика» мамандығының студенттері үшін арналған.
Рецензенттер:
Ибрагимов О.М. – ф.-м.ғ.к., М.Әуезов атындағы ОҚМУ, «Информатика» кафедрасының доценті;
Ержанов Н.Е. – ф.-м.ғ.к, доцент, Академиялық инновациялық университеті, «Бағдарламалау және есептуіш техникасы» кафедрасының меңгерушісі;
Ниязымбетов А.Д. – ф.-м.ғ.к, доцент, Академиялық инновациялық университет, «Информатика» кафедрасыңмеңгерушісі
«Информатика» кафедрасының жиналысымен (№ 1 хаттама «27» тамыз 2011 ж.)және жалпы педагогикалық факультеттің нұсқаулық комиссиясымен (№ 1 хаттама «28» тамыз 2011ж.) қарастырылып баспаға ұсынылған.
М.Әуезов атындағы ОҚМУ Әдістемелік кеңесімен баспаға ұсынылған, протокол № ___ от «____» ______________ 2011 г.
© М.Әуезов атындағы Оңтүстік қазақстан мемлекеттік университеті, 2011ж.
Шығаруға жауаптыҚұрақбаев Ж.С.
1, 2 –дәрістер. Сызықтық программалау есебінің қойылуы. Сызықтық программалау есебінің геометриялық және экономикалық түсіндірмесі. Қарапайым экономикалық есептерді математикалық модельдеу. Теңсіздікті теңдікпен ауыстыру.
1 Жалпы түсініктемелер
2 Теңсіздіктерден теңдіктерге көшу
3 Теңсіздікті теңдікпен ауыстыру
4. Жай экономикалық есептердің математикалық
модельдерін құру.
Кіріспе
Қолданбалы математиканың ең маңызды саласының бірі – математикалық бағдарламалау; ол экстремальдық есептерді зерттеуге және олардың шешу әдістеріне арналған. Бұл пәнді оқу студентке қарапайым экономика есептерінің математикалық модельдерін құрастыруда алгашқы қадам жасауға, олардың математикалық қойылуы мен шешу әдістерін үйренуге мүмкіншілік береді.
Математикалық бағдарламалауды оқу кезінде алған білімін студент мамандығы бойынша экономика саласының есептерінің экономика – математикалық модельдерін құрастыру, осыдан алынатын математикалық есептерді қою, оның алгоритмін құрастыру және есептеу техникасын пайдаланып, шешімдерін табу үшін қолданады.
1 Сызықты бағдарламалау есептерін шешу. Жалпы түсініктемелер
Сызықтық программалау-белгісіздеріне сызықтық шектеулер қойылған, сызықтық функцияның ең кіші және ең үлкен мәндерін зерттеу және табу туралы ғылым.
Сызықтық функция
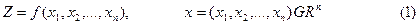
және сызықтық шектеулер
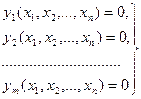 (2)
(2)
берілсін. Z-сызықтық функция болғандықтан, жалпы жағдайда 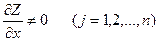 , олай болса қарастырылып отырғанаудан ішінде экстремалды нүктелер жоқ. Сондықтан сызықтық функцияның ең үлкен және ең кіші мәндерін ауданның шеткі нүктелерінен іздейміз. Бұл мәндерді табудасызықтық программалау есебін шығарудың арнайы әдістері қолданылады. Сызықтық функция Z-мақсат функциясы деп, ал сызықтық теңдеулер жүйесі (2) оның шектеулері деп аталады. Көптеген экономикалық есептер сызықтық программалау есептеріне келтіріледі.
, олай болса қарастырылып отырғанаудан ішінде экстремалды нүктелер жоқ. Сондықтан сызықтық функцияның ең үлкен және ең кіші мәндерін ауданның шеткі нүктелерінен іздейміз. Бұл мәндерді табудасызықтық программалау есебін шығарудың арнайы әдістері қолданылады. Сызықтық функция Z-мақсат функциясы деп, ал сызықтық теңдеулер жүйесі (2) оның шектеулері деп аталады. Көптеген экономикалық есептер сызықтық программалау есептеріне келтіріледі.
1.1 Жай экономикалық есептердің математикалық
модельдерін құру. Шикізатты қолдану есебі.
Екі түрлі зат өндіру үшін үш түрлі шикізат қолданылсын. Шикізат қорлары, өнімнің әр данасы үшін жұмсалатын шикізат көлемі және өнімнің әр данасын сату бағасы белгілі болсын. Өндірісті шикізат қорын тиімді пайдаланып, өнімді сатудан түсетін жиын пайда ең үлкен мән қабылдайтындай етіп ұйымдастыру керек.
| Шикізат түрлері | Өнім үшін жұмсалатын әр шикізат мөлшері | Шикізат қоры | |
| P1 | P2 | ||
| S1 S2 S3 | |||
| Бағасы |
Қойылған экономикалық есептің математикалық моделін түзейік.
Өндірілетін өнім мөлшерін х1 және х2 айнымалылары арқылы белгілесек, оны сатудан түсетін жиын Z=50x1+40x2®max, функциясымен, ал шикізат қорларын пайдалану
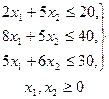
теңсіздіктер жүйесімен беріледі. Z-функциясы есептің мақсат функциясы, ал теңсіздіктер жүйесі оның шектеулері деп аталады.
Бұл есептің математикалық моделі.
Есепті n өнім өндіру үшін m шикізат түрін пайдаланғандағы жалпы түрде жазуға болады. Белгілеулер енгізейік 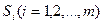 - шикізат түрлері,
- шикізат түрлері, 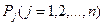 өнім түрлері, aij- j-ші өнімге жұмсалатын і-ші шикізат, xj- j-ші өнім мөлшері, cj- j-ші өнім сату бағасы. Онда есеп жалпы түрде былай беріледі:
өнім түрлері, aij- j-ші өнімге жұмсалатын і-ші шикізат, xj- j-ші өнім мөлшері, cj- j-ші өнім сату бағасы. Онда есеп жалпы түрде былай беріледі:
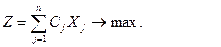 (1)
(1)
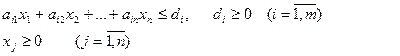 (2)
(2)
Рацион құру есебі.
Малды азықтандыру үшін екі түрлі жемдік заттар қолданылады. Олардың құрамына организмге қажетті үш түрлі тиісті мөлшерде нәрлі заттарды беру қажет. Жемдік заттардың құрамындағы нәрлі зат және әр малдың күнделікті нәрлі заттарды қабылдау мөлшері төмендегі кестеде көрсетілген
| Нәрлі заттар | Жемдік заттағы нәрлі зат мөлшері | |
| І | ІІ | |
| S1 S2 S3 | ||
| 1 кг қоректі зат құны |
Азықтандыру қажетті нәрлі заттар тиісті мөлшерде қабылданбай және бұған кеткен жалпы шығын барынша аз болатындай етіп ұйымдастыру қажет.
Математикалық тілде есеп былай жазылады:
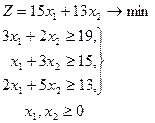
теңсіздіктер жүйесінің мақсат функциясына Z ең кіші мән беретін шешулерін табу керек.
Есептің жалпы түрін қарастырайық. Азықтандыруға қажетті m түрлі нәрлі заттары бар n түрлі жемдік заттарды алайық. Рацион дұрыс құрылу үшін қабылдайтын нәрлі заттар мөлшері кемімеуі тиіс. Олай болса bi- нәрлі заттар мөлшері, aij- j-ші түрдегі жемдік зат құрамындағы і-ші түрлі нәрлі зат мөлшері, сj- j-ші түрлі жемдік зат құны, хj- жұмсалатынын жемдік зат көлемі.
Сонымен, есеп былай жазылады:
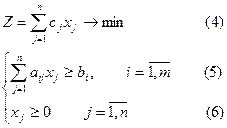
ІІ. Теңсіздіктерден теңдіктерге көшу.
Берілген теңсіздікті
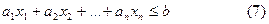
теңдікке келтіру үшін сол жағында қосымша оң таңбалы белгісіз қосамыз. Сонда (7) теңсіздігі мынадай түрге келеді:
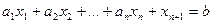 (8)
(8)
 (9)
(9)
мұндағы 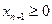 қосымша белгісіз.
қосымша белгісіз.
Теорема. (7) теңсіздігінің кез келген 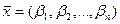 шешіміне сәйкес (8) теңдеуі және (9) теңсіздігінің бір ғана
шешіміне сәйкес (8) теңдеуі және (9) теңсіздігінің бір ғана 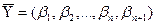 шешімі бар. Керісінше, (9) теңсіздігі және (8) теңдеуінің кез келген
шешімі бар. Керісінше, (9) теңсіздігі және (8) теңдеуінің кез келген 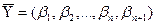 шешіміне сәйкес (7) теңсіздігінің бір ғана
шешіміне сәйкес (7) теңсіздігінің бір ғана 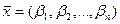 шешімі бар.
шешімі бар.
Дәлелдеуі. 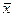 - (7) теңсіздігінің шешімі болсын. Онда
- (7) теңсіздігінің шешімі болсын. Онда 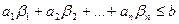
Теңсіздіктің сол жағын оң жағына аусытырып, оны 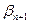 арқылы белгілейміз
арқылы белгілейміз
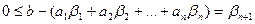
Онда 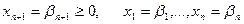 теңдеудің шешімі болады. Яғни
теңдеудің шешімі болады. Яғни
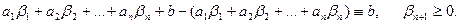
Керісінше, 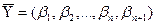 теңдеуін (8) шешімі болса, онда
теңдеуін (8) шешімі болса, онда 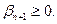
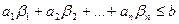
Теорема дәлелденді.
І. Шикізатты қолдану есебі.
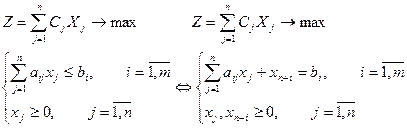
Рацион құру есебі.
3, 4 – ші дәрістер.Сызықты алгебралық теңдеулер жүйесін Жордан – Гаусс әдісімен шешу. Векторларды базиске бөлу, бір базистен екіншісіне өту.
1.3 Сызықтық теңдеулер жүйесін шешудің Жордан-Гаусс әдісі
Теңдеулер жүйесі төмендегідей берілсін:
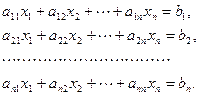 (1.3.1)
(1.3.1)
Мұндай теңдеулер жүйесін шешудің Жордан-Гаусс сандық әдісін пайдалану тиімді. Бұл сандық әдіс арқылы кері матрицаны да табуға болады. Сызықтық программалау есептерін шешуде көбіне Жордан-Гаусстың толық жою әдісін пайдаланады. Теңдеулер жүйелерінің бірінші теңдеуіндегі нөлге тең емес бір коэффициент таңдап алынады да, теңдеудің екі жағын сол коэффициентке бөлу арқылы таңдалған белгісіздің коэффициенті бірге келтіріледі. Қалған теңдеулерден осы айнымалыны жояды. Келесіде екінші теңдеуден нөлге тең емес бір коэффициент таңдалып, теңдеуді сол коэффициентке бөлу арқылы тиісті белгісіздің коэффициентін бірге келтіреді. Қалған теңдеулерден осы айнымалыны жояды. Осылайша барлық теңдеулерді қарастырады. Нәтижесінде жүйенің не үйлесімді, не үйлесімсіз екендігіне көз жеткіземіз. Егер теңдеулер жүйесі үйлесімді болса, онда шешімін табамыз. Мынадай жағдайлар кездесуі мүмкін:
1. Жүйені шешуде теңдеу нәтижесі 0=0 болса, онда теңдеуді жүйеден алып тастауға болады, себебі ол басқа теңдеулердің сызықтық комбинациясы.
2. Теңдеуден 0=bi шығатын болса, онда жүйе үйлесімсіз, шешімі жоқ.
Мысал. Жордан-Гаусс әдісін пайдаланып, есептің шешімін табамыз.
2x + у + 3z = -9,
8x + 3y + 5z = -13,
2x + 5y - z = -5.
Шешімі. Теңдңулер жүйесінің векторлық жазылуы:
xA1 + yA2 + zA3 = B.
бұл жерде
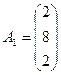 ,
, 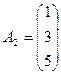 ,
, 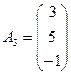 ,
, 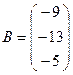 .
.
Кесте 3-Жордан-Гаусс әдісін кесте түрінде келтіреміз:
| A1 | A2 | A3 | B | Контр.  |
| -1 | -9 -13 -5 | -3 | ||
| ½ -1 | 3/2 -7 -4 | -9/2 | -3/2 | |
| -2 -32 | -23 | -15 | ||
| -2 -3 | -1 -2 |
x=1, y=-2, z=-3.
Векторларды базиске бөлу, бір базистен екіншісіне өту
n - өлшемді кеңестікте А1, А2,...., An+m векторлары берілсе, онда сызықтық тәуелсіз А1, А2,...., An векторлары базис құрайды. Жалпы түрде кез-келген тәуелсіз вектор n векторлар n - өлшемді кеңістіктің базисін құрайды. Бір базистен екінші базиске көшуге болады. Базисті табу, базистен базиске көшу операциялары Жордан – Гаусс әдісімен оңай орындалады.
1- мысал.
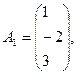
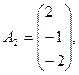
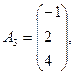
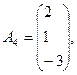
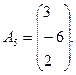
Берілген векторлар жүйесінде бір базисті тауып, одан екінші базиске көшу, Жордан-Гаусс әдісін кесте түрінде келтірейік:
| А1 | А2 | А3 | А4 | А5 |
| -2 | -1 -2 | -1 | -3 | -6 |
| -8 | -1 | -9 | -7 | |
| -5/7 5/3 13/21 | -7 |
Бірінші базис Б1= (А1, А2, A3). Осы базис арқылы А4, А5 векторлары былай жазылады:
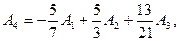
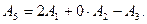
Б1 базистен Б2 базисіне көшу:
| А1 | А2 | А3 | А4 | А5 |
| -1 | 11/21 5/3 -13/21 |
Екінші базис Б2= (А1, А2, A5) арқылы А3 және А4 векторлары былай өрнектеледі:
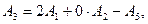
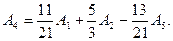
5, 6 – ші дәрістер.Сызықты бағдарламалаудың жалпы түсінігі. Есепті түрлендіру. Жазудың векторлық түрі. Жазудың матрицалық түрі. Сызықты бағдарламалау есебінің геометриялық интерпретациясы. Сызықты бағдарламалаудың графикалық әдіспен шешілуі. Графикалық әдіспен шешілетін есептерге мысалдар. Шикізатты қолдану есебі. Рационды құру есебі.
1.5 Сызықтық программалаудың жалпы есебі.
І. Есептің қойылуы.
Сызықтық функцияға
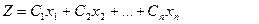 (1)
(1)
экстремум мәнін беретін сызықтың теңдеулер жүйесінің
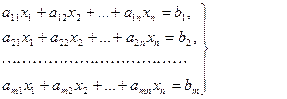 (2)
(2)
оң таңбалы
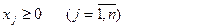 (3)
(3)
шешімдерін табу есебін сызықтық программалаудың жалпы есебі деп айтамыз. Мұндағы aij, bi, cj берілген тұрақтылар, bi-лерді оң таңбалы деп қарастыруға болады.
Сызықтық программалау есебінің (1)-(3) бірнеше түрдегі жазылуларын көрсетейік:
Векторлық түрдегі жазылуы:
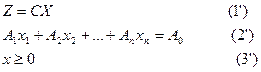
Мұндағы  n-өлшемді, ал A0 m-өлшемді векторлар.
n-өлшемді, ал A0 m-өлшемді векторлар.
Матрицалық түрдегі жазылуы
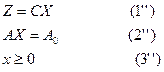
Қосынды белгісімен жазылуы
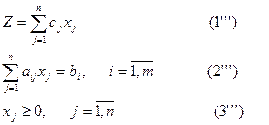
1.6 Сызықтық программалау есебін графиктік
әдіспен шешу
Графиктік әдіс сызықтық программалау есебінің геометриялық мағынасына негізделіп, көбіне екі өлшемді кеңестік есептерін және үш өлшемді кеңістіктің есептерін шешуде қолданылады, себебі жартылай кеңістіктердің қиылысынан тұратын шешімдер көпжағын құрудың жеткілікті ауыртпалығы бар.
Сызықтық программалау есебі екі өлшемді кеңістікте берілсін, яғни шектеулері екі айнымалыдан болсын
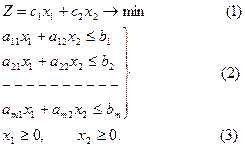
Жүйе (2), (3) үйлесімді, шешімдер көпбұрышы шектеулі делік. Әрбір теңсіздік (2), (3) жарты жазықтықты шеттік түзулерімен 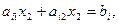
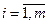
 бірге анықтайды.
бірге анықтайды.
Шектеулер жүйесінің шешімдер көпбұрышын (2) және сызықтық функцияның (1) Z=0 мәніндегі графигін тұрғызайық. Онда қойылған сызықтық программалау есебіне мынадай геометриялық мағына беріледі. 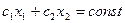 тірек түзуі және мұнда функция Zmin мәнін қабылдайтын шешімдер көпбұрышының нүктесін табу керек.
тірек түзуі және мұнда функция Zmin мәнін қабылдайтын шешімдер көпбұрышының нүктесін табу керек.
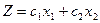 мәндері
мәндері 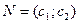 векторы бағытында өсетіндіктен, Z=0 түзуін N бағытында өзін-өзін параллель жылжытамыз.
векторы бағытында өсетіндіктен, Z=0 түзуін N бағытында өзін-өзін параллель жылжытамыз.
Сурет 1-ден шешімдер көпбұрышының екі тірек түзуі (А және С нүктелерінде) болатындығын, әрі min мәні қабылданатын A(x1;x2) нүктесінің координаталарын АВ және АЕ түзулерінің теңдеулер жүйесін шешу арқылы табу керектігін көреміз.
Егер шешімдер көпбұрышы шектеусіз облыс болса, екі жағдай мүмкін.
1-жағдай. 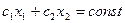 түзуі N векторы бағытында немесе оған қарама-қарсы бағытта қозғала отырып шешімдер көпбұрышын кесіп отырады және бірде-бір нүктесінде оған тірек болмайды. Бұл жағдайда сызықтық функция шешімдер көпбұрышында жоғарыдан да, төменнен де шектеусіз (сурет 2).
түзуі N векторы бағытында немесе оған қарама-қарсы бағытта қозғала отырып шешімдер көпбұрышын кесіп отырады және бірде-бір нүктесінде оған тірек болмайды. Бұл жағдайда сызықтық функция шешімдер көпбұрышында жоғарыдан да, төменнен де шектеусіз (сурет 2).


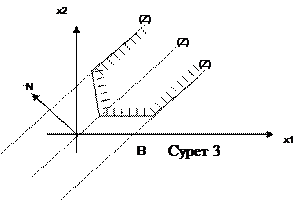
2-жағдай. Түзу қозғала отырып, шешімдер көпбұрышына тірек болды (сурет 3). Онда облыс түріне байланысты сызықтық функция жоғарыдан шектеулі және төменнен шектеусіз (сурет 3а), төменнен шектеулі және жоғарыдан шектеусіз (сурет 3б) немесе жоғарыдан да, төменнен де шектеулі (сурет 3в) болуы мүмкін.
Мысалдар. Шикізатты пайдалану есебі.
Екі түрлі P1, P2 өнім шығару үшін үш түрлі шикізат S1, S2, S3 қолданылады. Шикізат қорлары, әрбір өнімнің бір өлшемі үшін жұмсалатын әрбір шикізат шамасы және өнімнің бір өлшемін өткізуден түсетін пайда шамасы кестеде көрсетілген. Өнімді max пайда алатындай етіп, ұйымдастыру қажет
| Шикізат түрлері | Шикізат қоры | Өнім өлшемін жасауға жұмсалатын әр шикізат мөлшері | |
| P1 | P2 | ||
| S1 S2 S3 | |||
| Өнім өлшемінен түсетін пайда |
Шешуі. Р1-ден х1, Р2-ден х2 мөлшерінде өнімдер дайындалсын. Өнімнің бір өлшем шамасын дайындауда жұмсалатын шикізаттар мөлшерін және олардың қорларын ескерсек келесі шектеулер жүйесін аламыз
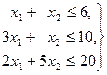
Есептің мақсаты, өнімдерді өткізуден түсетін max пайданы, екі айнымалының х1 және х2 функциясы деп қарастырамыз. Р1 өнімнің х1 мөлшері өткізгенде 10х1, Р2 өнімнің х2 мөлшері өткізгенде 8х2, барлығы, қосындыда 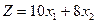 пайда келтіреді. Сонымен, шектеулер жүйесінің
пайда келтіреді. Сонымен, шектеулер жүйесінің
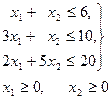
Сызықтық функция 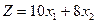 мәнін қабылдайтын нақты
мәнін қабылдайтын нақты  шешімдерін табу керек. Шешімдер көпбұрышын шекаралық түзулер арқылы
шешімдерін табу керек. Шешімдер көпбұрышын шекаралық түзулер арқылы
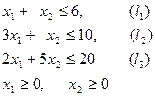
тұрғызамыз.
N=(10;8) векторын және
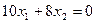 (Z) түзуін тұрғызамыз.
(Z) түзуін тұрғызамыз.
(Z) түзуін өзіне-өзін паралель N векторы бағытында жылжыта отырып, шешімдер көпбұрышының В нүктесінде тірек түзуіне айланып, бұл нүктеде функция Zmax мәнін қабылдайтынын көреміз.
В нүктесі (l2) және (l3) түзулердің қиылыснда жатқандықтан, оның координаталарын теңдеулер жүйесін
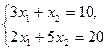 шешіп табамыз
шешіп табамыз 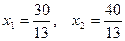 . Есептің оптималдық шешімі
. Есептің оптималдық шешімі 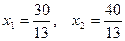 ,
, 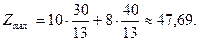
Сонымен 47,69т. көлеміндегі пайда келтіру үшін 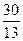 мөлшерінде Р1,
мөлшерінде Р1, 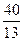 мөлшерінде Р2 өнімдерін шығаруды жоспарлау тиімді.
мөлшерінде Р2 өнімдерін шығаруды жоспарлау тиімді.
1.7 Сызықтық программалау есебін n-m=2 болғанда
графиктік әдіспен шешу
Сызықтық программалау есебін қарастырайық
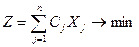 (1)
(1)
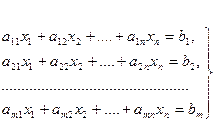 (2)
(2) 
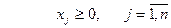 (3)
(3)
Бұндағы барлық теңдеулер сызықтық тәуелсіз және n-m=2 қатынасы орындалсын.
Жордан-Гаусс әдісімен m жою барысында алғашқы m айнымалылар 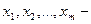 базистік, ал соңғы екі айнымалы
базистік, ал соңғы екі айнымалы 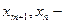 еркін айнымалыларға айналсын делік, яғни шектеулер (2) мына түрге келтірілсін
еркін айнымалыларға айналсын делік, яғни шектеулер (2) мына түрге келтірілсін
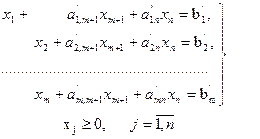 (4)
(4)
Түрленген жүйе (4) теңдеулері арқылы сызықтық функцияны тек еркін айнымалылармен өрнектейміз де, базистік айнымалыларды 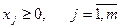 шығарып тастап, теңсіздіктермен берілген шектеулерге көшеміз. Ақырында келесі есепті аламыз
шығарып тастап, теңсіздіктермен берілген шектеулерге көшеміз. Ақырында келесі есепті аламыз
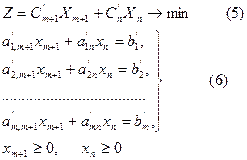
Бұл есепте екі айнымалы ғана болғандықтан графиктік әдіспен шеше аламыз. Оптималдық 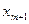 және
және 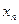 мәндерін тауып, (4)ге қою арқылы,
мәндерін тауып, (4)ге қою арқылы, 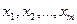 оптималдық мәндерін табамыз.
оптималдық мәндерін табамыз.
Мысал. Графиктік әдіспен есептің оптималдық шешімін табу керек.
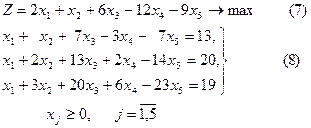
Шешуі. Жордан-Гаусс толық жою әдісімен иеңдеулер жүйесін түрлендіреміз
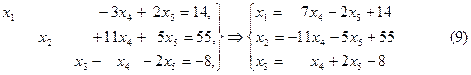
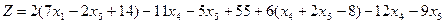 мұндағы
мұндағы 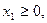
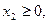
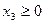 базистік айнымалыларды теңдеулерден алып тастасақ, есеп графиктік әдіспен шешуге болатын мына түрге келеді:
базистік айнымалыларды теңдеулерден алып тастасақ, есеп графиктік әдіспен шешуге болатын мына түрге келеді:
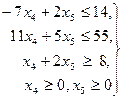 (11)
(11)
Шешімдер көпбұрышын ABCD және сызықтық функцияны 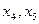 координаталар жүйесінде тұрғызамыз.
координаталар жүйесінде тұрғызамыз. 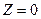 түзуін
түзуін 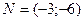 векторының бағытында жылжыта отырып, шешімдер көпбұрышының AD қабырғасында сызықтық функция Z-тің max мәнін көреміз. А(0;4) немесе D нүктелерінің координаталары арқылы
векторының бағытында жылжыта отырып, шешімдер көпбұрышының AD қабырғасында сызықтық функция Z-тің max мәнін көреміз. А(0;4) немесе D нүктелерінің координаталары арқылы 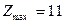 мәнін табамыз. Бастапқы есептің оптималдық шешімін табу үшін
мәнін табамыз. Бастапқы есептің оптималдық шешімін табу үшін 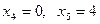 мәндерін (9)-ге қоямыз. Нәтижесінде
мәндерін (9)-ге қоямыз. Нәтижесінде 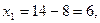
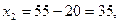
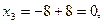
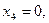
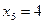 оптималдық шешімін табамыз.
оптималдық шешімін табамыз.
7, 8 – ші дәрістер.Сызықты бағдарламалау есебі үшін Симплекс әдісі. Сызықты бағдарламалау есебін Симплекс әдісін қолданып шешу. Тіреу планын түзу. Оптималды планды іздеу. Оптималдық шарты. Симплекс әдісінің алгоритмі.
Сызықтық программалау есебінің оптималдық шешімі тірек шешімдерінің ішінен іздестірімді, әрбір тірек шешімі берілген n векторлар 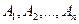 жүйесіндегі m сызықтық тәуелсіз векторлармен анықталатындықтан, олардың саны
жүйесіндегі m сызықтық тәуелсіз векторлармен анықталатындықтан, олардың саны 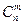 терулерінің санынан аспайды.
терулерінің санынан аспайды.
m және n сандары жеткілікті үлкен болғанда оптималдық шешімді барлық тірек шешімдерін құру арқылы іздестіру өте қиын.
Симплекс әдісі белгілі тірек шешімінен келесі жақсартылған тірек шешіміне көшіріп отырады, санаулы қадымнан соң оптималды шешімге келтіреді, есептің шешімі жоқ немесе сызықтық функциясы шектеусіз болса, оны да көрсетеді.
1. Тірек шешімдерін құру.
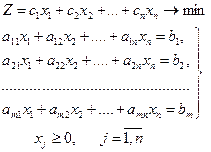
есебін қарастырайық және мұндағы 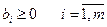 болсын.
болсын.
Шектеулер жүйесінің алғашқы m векторлары бірлік векторлар болсын делік. Онда есеп мына түрде қойылады
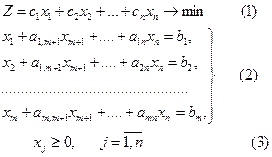
теңдеулер жүйесін (2) векторлық түрде жазайық
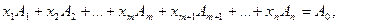 (4)
(4)
мұндағы
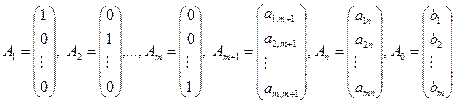
m- өлшемді кеңістіктің сызықтық тәуелсіз 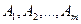 векторлары осы кеңістіктің базисін жасайтындықтан, (4) жіктелуіндегі
векторлары осы кеңістіктің базисін жасайтындықтан, (4) жіктелуіндегі 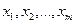 айнымалыларын базистік деп,
айнымалыларын базистік деп, 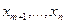 еркін айнымалыларын нөлге теңестіріп,
еркін айнымалыларын нөлге теңестіріп, 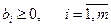 болғандықтан алғашқы
болғандықтан алғашқы
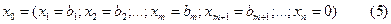
шешімін аламыз. Осы шешімге сәйкес
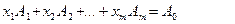 (6)
(6)
жіктелуіндегі 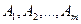 векторлары сызықтық тәуелсіз, демек құрылған алғашқы шешім есептің тірек шешімін береді.
векторлары сызықтық тәуелсіз, демек құрылған алғашқы шешім есептің тірек шешімін береді.
Бастапқы тірек шешімнен (5) келесі тірек шешімді қалай құратындығын қарастырайық. m-өлшемді кеңістіктің (4) өрнектегі әрбір вектроы базистік 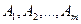 векторлары арқылы бір ғана түрде былай жіктеледі
векторлары арқылы бір ғана түрде былай жіктеледі
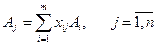
Базиске енбеген, мысалы 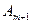 векторының,
векторының,
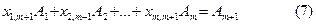
әйтеуір бір коэффициенті 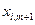 оң таңбалы болсын делік. Әзірге белгісіз
оң таңбалы болсын делік. Әзірге белгісіз 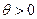 шамасына (7) теңдікті көбейтіп, (6) теңдіктен шегерсек,
шамасына (7) теңдікті көбейтіп, (6) теңдіктен шегерсек,
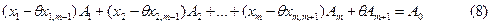
теңдігін аламыз. Сонымен
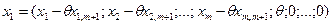 векторының компоненттері теріс таңбалы болмаса, шешімді береді.
векторының компоненттері теріс таңбалы болмаса, шешімді береді. 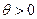 болғандықтан,
болғандықтан, 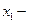 векторының теріс таңбалы
векторының теріс таңбалы 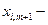 лер енетін компоненттері теріс таңбалы бола алмайды. Сондықтан кез келген
лер енетін компоненттері теріс таңбалы бола алмайды. Сондықтан кез келген 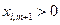 үшін
үшін 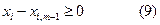
болатындай 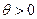 мәнін табу қажет. (9) теңсіздіктен
мәнін табу қажет. (9) теңсіздіктен 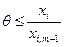 демек
демек 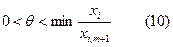
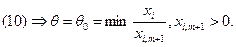
Оптималдық шешімді табу. Оптималдық шарттары.
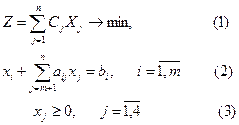
есебінің шешімдері бар және әрбір тірек шешімі құнарлы делік. Онда
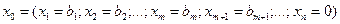
тірек шешіміне
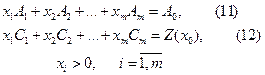
ал кезкелген 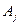 векторына берілген
векторына берілген 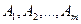 базисінде
базисінде
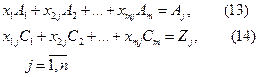
теңдіктері тиесілі.
Сызықтық функцияның 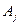 векторына сәйкес коэффициентін
векторына сәйкес коэффициентін 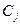 деп белгілейміз. Онда келесі теорема орындалады.
деп белгілейміз. Онда келесі теорема орындалады.
Теорема1. Егер әйтеуір бір 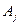 векторына
векторына 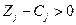 шарты (белгісі) орындалса, онда
шарты (белгісі) орындалса, онда 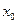 шешімі оптималды емес және
шешімі оптималды емес және 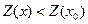 теңсіздігі орындалатын ч шешімін құруға болады.
теңсіздігі орындалатын ч шешімін құруға болады.
Салдар. Егер әйтеуір бір шешім  дің базисінде барлық
дің базисінде барлық 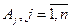 векторларының жіктелуіне
векторларының жіктелуіне
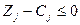 (18)
(18)
шарты (белгісі) орындалса, онда шешім 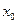 оптималды. Сызықтық функцияның min мәнін табу есебінің оптималдық шарты (белгісі) (18) теңсіздіктерімен анықталады, ал
оптималды. Сызықтық функцияның min мәнін табу есебінің оптималдық шарты (белгісі) (18) теңсіздіктерімен анықталады, ал 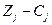 мәндері шешім бағалары деп аталады.
мәндері шешім бағалары деп аталады.
Сонымен, сызықтық функция min-мын табу есебінің шешімі оптималды болуы үшін оның бағаларының оң таңбалы болмауы қажетті және жеткілікті.
Сызықтық программалаудың сызықтық функция max-мын табу есебі үшін келесі теорема орынды.
Теорема2. Егер әйтеуір бір 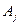 векторына
векторына 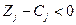 шарты (белгісі) орындалса, онда
шарты (белгісі) орындалса, онда 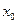 шешімі оптималды емес және
шешімі оптималды емес және 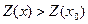 болатын х шешімін құруға болады.
болатын х шешімін құруға болады.
Салдар. Егер әйтеуір бір шешім 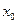 дің базисінде барлық
дің базисінде барлық 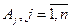 векторларының жіктелулеріне
векторларының жіктелулеріне
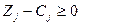 (19)
(19)
шарты (белгісі) орындалса, онда шешім 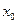 оптималды.
оптималды.
(19) теңсіздіктері сызықтық функцияның max мәнін табу есебінің оптималдық шарты (белгісі).
Сонымен, сызықтық функция max-мын табу есебінің шешімі оптималды болуы үшін оның бағаларының теріс таңбалы болмауы қажетті және жеткілікті.
Симплекс әдісінің алгоритмі.
Теоремалар 1,2 және олардың салдарынан алғашқы тірек шешімінен бастап оптималды шешіммен аяталатын тірек шешімдер тізбегін алуға болады.
Тірек шешімі
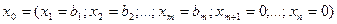
m- өлшемді бірлік (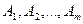 ) векторларына тиісті, сызықтық функцияның min мәнін іздестіретін, (1)-(3) сызықтық программалау есебін қарастыруды жалғастырайық.
) векторларына тиісті, сызықтық функцияның min мәнін іздестіретін, (1)-(3) сызықтық программалау есебін қарастыруды жалғастырайық.
Тірек шешімін оптималдыққа зерттеу үшін 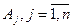 векторларын базиске жіктеп, бағалар
векторларын базиске жіктеп, бағалар 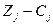 мәндерін есептейміз. Базис бірлік болғандықтан
мәндерін есептейміз. Базис бірлік болғандықтан 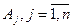 векторларының жіктелу коэффициенттері олардың компоненттеріне тең
векторларының жіктелу коэффициенттері олардың компоненттеріне тең 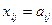 .
.
Бірінші тірек шешімін анықтаған соң, есептің шарттары мен бастапқы берілгендерін жазып, әрі қарай есептеулерді арнайы симплекс кестесімен жүргізу ыңғайлы. Сызықтық функцияның базистік векторларға тиісті коэффициентерін С бағанына, есептеу барысында оптималдық шешімге айналатын 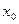 тірек шешімін
тірек шешімін 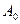 бағанына, әрі қарай
бағанына, әрі қарай 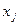 ден белгіленетін j-ші вектордың базиске жіктелу коэффициентерін
ден белгіленетін j-ші вектордың базиске жіктелу коэффициентерін 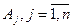 болғандарына жазамыз.
болғандарына жазамыз.
m+1 жанының 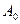 бағанына сызықтық функцияның табылған тірек шешіміндегі мәні
бағанына сызықтық функцияның табылған тірек шешіміндегі мәні 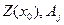 болғандарына бағалар мәндері
болғандарына бағалар мәндері 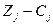 жазылады.
жазылады. 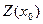 және
және 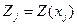 -лер сызықтық функцияға тірек шешім компоненттерін және j-ші вектордың базиске жіктелу коэффициенттерін қою арқылы есептелінеді, кестеде бұл мәндер келесі скалярлық көбейтінділермен алынады
-лер сызықтық функцияға тірек шешім компоненттерін және j-ші вектордың базиске жіктелу коэффициенттерін қою арқылы есептелінеді, кестеде бұл мәндер келесі скалярлық көбейтінділермен алынады
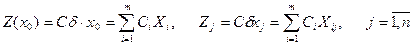
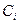 -сызықтық функцияның базистік векторларға тиісті коэффициентері.
-сызықтық функцияның базистік векторларға тиісті коэффициентері.
 2015-05-14
2015-05-14 2796
2796







