Коммивояжер /сауда агенті/ есебі

1)Коммивояжер қаланы аралап шығуы керек. Бірақ ол әрбір қалада бір рет қана болуы қажет және бастапқы қаласына қайтып оралуы керек. Әр қалалар арасындағы жолының уақыты белгілі. Бұл есепте жол жүру уақыттарьның қосындысы ең аз болуы үшін оптималды шешімін табу керек.

1) 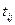- 1 қаласынан j қаласына дейінгі жол жүру уақыты.

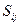- жол ақысы.

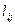- жол ұзындығы.

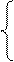
1, егер і-дан j-ға барса, і j

X_ij=

0, егер і-дан j –ға барса, і j

1) бір қалаға бару.

2) бір қалада бір рет болу.

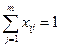
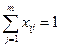
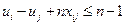
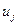-қадам, 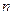- қадамдардың саны.

Бүтін санды сызықты программалау есептерін шығару әдістері хақында.

Экономикалық есептердің біразында бүтін сандық шешімдер талап етіледі. Мысалы, кәсіпорындар арасында өндірістік тапсырмалардың бөлінді, бұйымдарды пішу, құралдары жұмысқа қосу, кемелерді самолеттерді (ұшақтарды) сапарларға бөлу, тағы сол сияқты есептерде бүтін сандық шешімдер қажет.Бірлік барлық өндіріс көлемінің жеткілікті аз бөлігін құраса, оптималдық шешімді кәдімгі симплекс әдісімен тауып, бүтін сандық түрге жуықтауға болады.

1. Есептің қойылуы. Сызықтық функцияның

Z =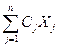

минималды мәнін

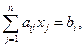
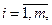
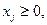x_j – бүтін,

шектеулерде табу керек.

Жалпы шектеулерге қосымша бүтін сандық шектеулер дөңес шешімдер жиынын кеңейтіп, геометриялық тұргыдан сызықтық программалаудың келесі қасиеттері бар есебін береді:

1) жаңа шешімдер көпжағы алғашқы шешімдер көпжағының барлық бүтін нүктелерін қамтиды;

2) сызықтық функция оптималдық мәнін бұрыштық нүктеде ғана қабылдайтындықтан, осындай көпжақты құру арқылы бүтін сандық оптималдық шешім алынады. Геометриялық кескіні суретте көрсетілгендей. Есепті симплекс әдісімен шешіп, бүтін сандық шешім алынса доғарамыз. Шешімнің кемінде бір компоненті бөлшек сан болса, қосымша шектеу енгізіп, симплекс әдісін жалғастыратын әдісті Гоморі әдісі деп атайды.

2.1 Қосымша шектеуді құру

Оптималдық шешім x = (x₁, x₂, …, x_m, …, x_n) оның базисі A₁, A₂, …, A_і, …, A_m дейік. Онда соңғы симплекс кесте мына түрге келеді

X_і – бөлшек болсын, онда кейбір x_іj – лерде бөлшек сандар болуы қажет, әйтпесе есептің бүтін сандық шешімі жоқ. Сандардың бүтін бөліктерін [x_і] және [x_іj] деп белгілейміз. Бұлар x_і және x_іj сандарынан аспайтын ең үлкен бүтін сандар. Онда сандардың бөлшек бөліктері q_і және q_іj – лер теріс таңбалы емес келесі айырымдармен анықталады:

X_і – [X_і] = q_і, x_іj - [x_іj] = q_іj.

Шарт бойынша x_j 0; бүтін сандар, онда келесі айырым да

[(q_і1x₁ + q_і2x₂ + …. + q_іnx_n) - q_і ] 0

бүтін сан болады.

Бұл теңсіздікті x_n+1 0 қосымша айнымалысын енгізумен тендеуге келтіріп, тендеудің еқі жағын да (-1) – ге көбейтіп, соңғы симплекс кестесіне тіркейміз. Кеңейтілген симплекс кестесіне қосалқы симплекс әдісін қолданамыз. Алынған шешім бүтін санды болмаса жаңадан қосымша шектеу жасалып, жоғарыдағы әрекет қайталанады.

Оптималдық шешімде бірнеше x_і бөлшек болса, қосымша шектеу

maxq_і – ге жасалады.

Есепті шешу бүтін сандық шешім немесе бүтін сандық шешім жоқтығы алынғанда тоқталады.

Бүтін сандық шешім жоқ, егер x_і бөлшегінде барлық x_іj - лер бүтін болса.

29, 30 – ші дәрістер. Ойындар классификациясы. Коалициясыз ойындар, тепе-теңдік ахуалы. Матрицалық ойындардың кеңейтілуі, тиімді стратегиялар.

Ойын теориясының пәні, негізгі ұғымдары

Белгісіздік жағдайында шешім қабылдау – тиімді шешімдер теориясының бір міндеті. Шешімді дәйектеу үшін ойындар теориясында арнайы математикалық әдістер құрылған. Ойындар теориясы жас математикалық пәндерге жатады. Оның қалыптасуы 1944 ж. Нейман мен Моргенштернның «Ойындар және экономикалық мінез-құлық теориясы» монографиясының шығуымен байланысты. Осылайша ойындар теориясы практикалық қосымшасы бар математикалық бағытқа айналды.

Ойындар теориясы бұл – математикалық модельдер теориясы. Онда қатысушылардың қызығушылығы әртүрлі, алға қойған мақсаттарына олар әртүрлі жетеді. Қатысушылардың қарама-қарсы қызығушылықтарының соқтығысуы қақтығыс жағдайының туындауына алып келеді. Мұндай жағдайларды талдау қажеттілігі өз кезегінде ойындар теориясының туындауына алып келеді. Көптеген маңызды емес себептерге байланысты практикалық қақтығыс жағдайын талдау кезінде туындайтын қиындықтарды болдырмау үшін жағдайдың оңайлатылған моделі құрылады. Мұндай модель ойын деп аталады. Ойын моделінде қақтығыс жағдайы белгілі бір ережеге сай өрбиді. Қақтығыс жағдайын анализдеудің табиғи қоры ретінде кеңінен таралған ойындар қолданылады. Олар: шахмат, шашка, карталық ойындар. Сондықтан ойын теориясына келесі терминдер сай келеді: «ойыншылар» (қақтығысқа қатысатын екі жақ), «ұтыс» (қақтығыстың бітуі) және т.б.

Ойын шешімінің белгісіздігі әр түрлі себептерден туындайды. Оларды 3 топқа бөлуге болады:

1. Ойын ережесінің ерекшеліктері ойын дамуының әртүрлілігін туындатады, сондықтан ойынның қалай бітуін болжау мүмкін емес. Мұндай түрдегі белгісіздіктің қайнар көзі комбинаторлық деп аталады, бұған сәйкес ойындарда комбинаторлық деп аталады. Бірақ комбинаторлық ойын қиындығы тиісті математикалық құралмен есептеуіш техника қолданылған арнайы тарихи ауыспалы мінез-құлыққа ие. Аса қиын емес логикалық есептерді шешу арқылы біртұтас комбинаторлық ойындардың ұтысты комбинациялары табылған.

2. Келесі белгісіздіктің қайнар көзі болып, ықпал ететін кездейсоқ факторлар жатады. Кездейсоқ себептерге байланысты нәтижесі белгісіз болған ойындар азартты деп аталады (сүйек ойыны, тиынның қай жағы түсетініне байланысты ойын, рулетка).

3. Үшінші белгісіздік қайнар көзі қарсыластардың іс-қимылдары туралы мәліметтердің жоқтығынан тұрады. Мұндай ойын түрін стратегиялық деп атайды.

Осы ойындарды жете қарастырсақ. Ойында екі немесе бірнеше қарсыластардың қызығушылықтары соқтығысуы мүмкін. 1-ші жағдайда ойын – жұпты, 2-шісінде көпшілікті деп аталады. Жұпты ойындардың практикалық маңызы үлкен болғандықтан тек соны ғана қарастырамыз. Ойынға қатысушыларды А және В арқылы белгілейміз. Сондай-ақ, ойынға дейін нақты құрастырылған ережеге сәйкес А және В ойыншыларының іс-әрекетінің ретін келісіп аламыз. Ереже мынаны анықтайды: ойыншылардың мүмкін іс-қимылдардың вариантын, ойын шешімін, ойындардың көпшілігінде қатысушылардың қызығушылығы сандық бейнелейге илігеді деп болжайды, яғни ойын нәтижесі (ұтысы) кейбір санмен анықталады. Ойын теориясында ойын ережесімен берілген бір іс-әрекетті таңдау және оны іске асыруды жүріс деп аталады. Ойыншының стратегиясы деп кез-келген мүмкін жағдайды және кез-келген іс-жүзіндегі ақпаратты таңдауға арналған жоспарды айтамыз. Әрине, ойыншы шешімді ойын барысында қабылдайды. Бірақ, теориялық тұрғыдан алғанда ойыншы шешімді алдын-ала қабылдайды. Сонда бұл шешімдердің жиынтығы оның стратегиясын құрайды. Мүмкін болған стратегиялардың санына байланысты ойындар шекті және шексіз болып бөлінеді. Ойын теориясының мақсаты – ойыншылар үшін нұсқау табу, яғни оларға тиімді стратегия анықтау. Тиімді стратегия деп, ойынның бірнеше рет қайталануында, ойыншыға орташа максимальді ұтысын қамтамасыз ететін стратегияны айтады. Ойын стратегиясының қарапайым түрі бұл – екі адамның нольдік ұтысты ойыны (екі жақтың да ұтыс жиыны нольге тең). Ойын 2 жүрістен тұрады: А ойыншысы өзінің 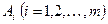мүмкін стратегиясының бірін таңдайды, ал В ойыншысы өзінің 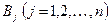стратегиясын таңдайды. Еске сала кететін жай әрбір таңдауды ойыншылар білмей жүргізеді. Ойыншылардың 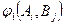және 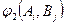ұтыстары

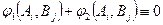(4.1)

арақатынасын қанағаттандырады.

Егер 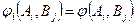болса, 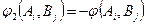аламыз.

А ойыншының мақсаты – 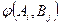функциясын максималдау, өз кезегінде, В ойыншының мақсаты – бұл функцияны минималдау. Әрбір ойыншы функцияның мәні тәуелді айнымалылардың бірін таңдай алады. Егер А ойыншы А_i стратегиясының бірін таңдаса, онда бұл өзінше 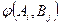функциясының мәніне ықпал ете алмайды. А_i –дің 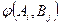мәнінің шамасына ықпалы анықталмаған болып табылады. Анықталғандық басқа ойыншымен B_j айнымалыны 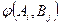-ні минималдау принципі негізінде таңдау нәтижесінде орын алады. 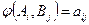болсын. А матрицасын құрамыз.

.

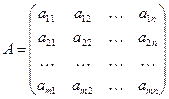Матрица қатарлары А_i стратегияларына сәйкес келеді. А матрицасы төлемді немесе ойын матрицасы деп аталады. Матрицаның a_ij элементі А ойыншының ұтысы, егер ол А_i стратегиясын, ал В ойыншысы B_j стратегиясын таңдаса. А ойыншысы кейбір А_i стратегиясын таңдаған болсын, сонда ең төмен жағдайда (мысалы, егер таңдау В ойыншысына белгілі болған жағдайда), ол 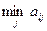-ге тең ұтыс алады. Мұндай мүмкіндікті болжамдап, А ойыншысы өзінің 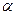минималды ұтысын максималдау стратегиясын таңдауы тиіс.

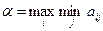. (4.2)

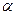шамасы – А ойыншының кепілденген ұтысы – ойынның төменгі бағасы деп аталады.

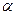– ны алуды қамтамасыз ететін 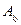стратегиясын максиминді деп айтамыз.

В ойыншысы стратегияны таңдау барысында сондай 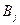стратегиясын таңдайды, оның ұтылысы матрицаның j бағанының элементтер мәнінің максималдығынан аспайды, яғни кіші немесе тең 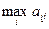. j- нің әртүрлі мәні үшін 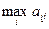жиынын қарастырсақ. В ойыншысы әрине өзінің 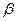максимальді ұтылысын минималдайтын j мәнін таңдайды.

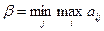. (4.3)

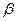шамасы ойынның жоғары бағасы деп аталады, ал 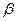ұтысқа сәйкес B_j стратегиясын минимаксті деп айтамыз. Іс жүзінде А ойыншының ұтысы, әріптестердің іс-әрекеті нәтижесінде, төменгі және жоғарғы ойын бағасымен шектелген. Егерде бұл өрнектер тең болса, яғни

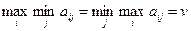, (4. 4)

онда А ойыншының ұтысы анықталған сан. Ондай ойын анықталған деп аталады. Ал (4.4) ұтысы ойын мәні деп аталады және матрицаның 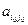элементіне тең. Толық анықталған ойынды кейде егер нүктесі бар ойын деп те атайды. Осындай ойын матрицасындағы 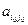элементі бір мезгілде i_o қатарында минимальді, j_o бағанында максимальді болып табылады және егер нүкте деп аталады. Егер нүктеге ойыншылардың оптимальді стратегиялары сәйкес келеді, бұл стратегиялар ойынның шешімін құрайды. Ойынның шешімі мына қасиетке ие: егер ойыншылардың бірі өзінің оптималды стратегиясын ұстанатын болса, онда келесі ойыншыға өз оптималды стратегиясынан ауытқуы ұтымды емес.

Мысал 1. А₁ және А₂ төлемді матрицаларымен берілген ойындар үшін төменгі және жоғарғы бағасын анықтау керек:

.

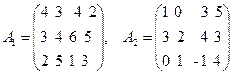Шешуі. А₁ матрицасындағы қатарларының a_ij минималды мәндері сәйкесінше 2, 3, 1- ге тең. Олардың ішіндегі максималды мәні 3-ке тең. Демек, 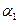– матрицасы А₁ болған ойынның төменгі бағасы – 3-ке тең.

β₁ –ді (осы ойынның жоғарғы бағасы) анықтау үшін матрица бағандарындағы максималды элемент мәнін табамыз. Бағандар бойынша мынау бар: 4, 5, 6, 5. Сәйкесінше, β₁ = 4. А₂ матрицасы үшін

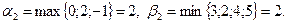
Осылайша, 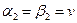– ойын бағасы. Осы ойынның шешілуі А ойыншысының А₂ стратегиясын таңдаудан тұрады, оның ұтысы 2-ден кем болмауы тиіс. В ойыншысы үшін оптималды стратегия В₂ болып табылады.

Ойыншылардың біреуінің оптималды стратегиясынан ауытқуы ұтыстың азаюына (А ойыншысы үшін) және ұтылыстың ұлғаюына (В ойыншысы үшін) алып келетінін байқау оңай.

Осылайша, егер ойын матрицасында егер нүкте бар болса, онда ойын шешімі белгілі. Әрбір ойыншы өзінің оптималды стратегиясын қолданады. Егер нүктесі жоқ матрицалар үшін ойын шешімін табу сұрақ туындайды. Бұл ойындарда 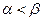. Әрбір ойыншылар үшін минимаксты стратегияларды қолдану 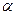-дан көп емес ұтысты және 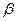-дан кем емес ұтылысты қамтамасыз етеді. Әрбір ойыншылар үшін ұтысты ұлғайту (ұтылысты азайту) жаратынды сұрақ. Бұл сұраққа жауап іздеп, ойыншылар бір емес бірнеше стратегияларды қолданады. Стратегияны таңдау кездейсоқ жағдайда болады. Ойыншының өз стратегиясын кездейсоқ таңдауы аралас стратегия деп аталады.

Минимакс теоремалары. Матрицалық ойындардың негізгі теоремасы.

Матрицасы 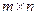өлшемді болған ойында А ойыншының стратегиясы Х = (х₁, х₂, …, х_m) ықтималдықтар тобымен беріледі. Бұл ықтималдықтармен ойыншы өзінің сәйкес алғашқы таза стратегиясын қолданады. Бұл топтарды компоненттері үшін келесі шарт орындалатын m- дік вектор ретінде қарастыруға болады:

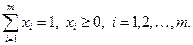(4.5)

Аралас стратегиясына сәйкес В ойыншысы үшін n -дік вектор 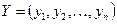дәл осылай анықталады. А және В ойыншылары стратегиясы үшін x_i және y_i ықтималдығы 0-ге тең болмаса, онда ол белсенді деп аталады.

Аралас стратегияны қолданғанда А ойыншының ұтысы ұтыстың математикалық күтімі ретінде анықталады, яғни мынаған тең 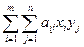немесе (векторлық-матрицалық жазуда) .

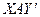Келесіден тұратын негізгі ойын теориясының теоремасы бар: Әрбір ақырлы ойынның кем дегенде бір шешімі бар, мүмкін, аралас стратегиялар облысында.

Оптималды стратегияны қолдану ойын бағасына тең ұтысты алуына мүмкіндік береді:

^.

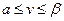Ойыншылардың оптималды стратегиялары үшін мына арақатынас орын алады:

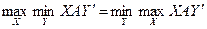(4.6)

Стратегиялар тиімділігінің қажетті және жеткілікті шарттары.

А ойыншының 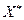оптимальді стратегиясын қолдануы оған В ойыншысының кез-келген іс-әрекетінде v ойын бағасынан кем емес ұтыспен қамтамасыз етеді. Сондықтан, келесі ара-қатынас орындалады:

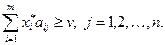(4.7)

В ойыншысы үшін 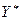оптимальді стратегиясы А ойыншының кез-келген стратегиясына v шамасынан артық емес ұтылысты қамтамасыз етеді. Яғни, мына ара-қатынас орынды.

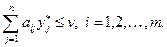(4.8)

Әрі қарай, (4.7) және (4.8) ара-қатынастары ойынды шешу үшін қолданылады.

Егер m, n мәндері үлкен болса, сондай-ақ, ойын матрицасында егер нүкте болмаса, онда ойын шешу мәселесі қиын. Сондықтан, матрицалық ойын теориясында бір ойынның шешілуі келесі жеңіл ойынның шешілуіне алып келетін тәсілдер қарастырылған. Қосалқы және біле тұра тиімді емес алғашқы стратегияны шегере отырып, матрицаның өлшемін қысқартуға болады. Қосалқы стратегиялар деп – төлемді матрицада бірдей элемент мәні сәйкес келетін стратегияларды айтамыз, яғни олар матрицадағы бірдей бағандарға (қатарларға) сәйкес. Егер матрицаның і қатарындағы барлық элементтер сәйкес k қатарындағы элементтерден кіші болса, онда А ойыншысы үшін і- ші стратегиясы біле тұра тиімді емес деп аталады. Егер матрицаның r бағанындағы элементтер сәйкес j бағанындағы элементтерден үлкен болса, онда В ойыншысы үшін В_r стратегиясы – біле тұра тиімді емес. Мысалы, А₂ матрицасында В ойыншысы үшін алдын-ала белгілі тиімді емес 4 стратегия, себебі а_і4 мәні сәйкес бірінші және екінші баған мәнінен аспайды. Матрицаның 4 бағанын алып тастауға болады. (В ойыншысы ешқашан бұл стратегияны қолданбайды).

Қатар және баған элементтерінің суммасы тең ішкі матрицаларға бөлу арқылы матрица өлшемін қысқартуға болады. Сонда матрицаға таза стратегияның орнына аралас қосылады. Аралас стратегияға сәйкес матрица элементтері сәйкес элемент қосындыларын аралас стратегияға біріктілген таза стратегия санына бөлу арқылы табылады. Егер аралас стратегиялар оптималдылар қатарына кірсе, онда оған кіретін таза стратегиялардың қолдану ықтималдығы өзара тең.

Қатар және баған бойынша элементтер қосындылары тең, 4 ішкі матрицаларға бөлінген А₃ матрицасын қарастырамыз:

.

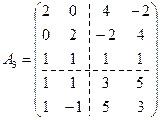А₁, А₂ және А₃, А₄ және А₅, В₁ және В₂, В₃, сондай-ақ В₄ стратегияларын біріктіріп, матрицаны мына түрге келтіреміз.

.

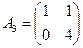Алынған матрицада егер нүкте бар. Сондықтан А₂ матрицасымен берілген алғашқы ойын шешімі мынадай: X*=(1/3; 1/3; 1/3; 0; 0), Y*=(1/2; 1/2; 0; 0). Ойын бағасы 1-ге тең. Ойынды оңайлату нәтижесінде оның шешімі анық болды.

А ойыншысы үшін оптималды стратегиялар комбинациясы А₁, А₂ және А₃ болады, ал В ойыншысы үшін стратегиялар комбинациясы В₁ және В₂. А₁, А₂ және А₃ стратегияларын қолдану ықтималдығы өзара тең және олардың қосындысы 1-ге тең, сондықтан X*=(1/3; 1/3; 1/3; 0; 0). В ойыншысы үшін оптималды стратегия түрі мынадай: Y*=(1/2;1/2; 0; 0).

Осылайша, 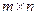ойынын шешкенде мынаны ескеруіміз керек:

а) Матрицада егер нүктенің бар жоқтығын тексеру;

б) егер мұндай нүкте жоқ болса, онда қосалқы және алдын-ала тиімді емес стратегияларды алып тастау үшін өзара қатар және баған элементтерін салыстыру керек;

в) кейбір таза стратегиялар тобын араласқа ауыстыру үшін матрицаларды ішкі матрицаларға бөлу мүмкіндігін қарастыру керек.

Ең қарапайым матрицалық ойын – бұл әрбір ойыншының екі стратегиясының болуы. А ойынының матрицасының түрі мынадай:

.

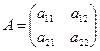Егер орынды нүкте жоқ болса, онда ойын шешімі X=(x₁, x₂), Y=(y₁, y₂) аралас стратегиялары болады.

Негізгі ойын теориясының теоремасына сәйкес, X=(x₁, x₂) оптималды стратегиясы қолдану А ойыншысына В ойыншысының кез келген стратегиясында v ұтысты қамтамасыз етеді. В ойыншысы үшін де оптималды стратегиясы аралас. Сондықтан егер А ойыншысы өзінің оптималды стратегиясын қолданса, онда бұл орайда В ойыншысы таза стратегиялардың бірін қолданады, бірақ А ойыншысының ұту шамасы өзгермейді. Теңдеулер жүйесін жазамыз:

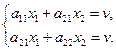(4.9)

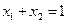болғандықтан шешім мынадай:

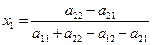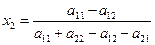, . (4.10)

х₁ және х₂ мәндерін (4. 9) теңдеулерінің біріне қоя отырып, мынаны аламыз:

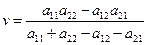. (4.11)

Осындай теңдеулер жүйесін құру арқылы В ойыншысы үшін оптималды стратегиясын табуға болады:

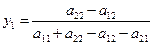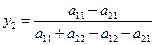, . (4.12)

Мысал 2. 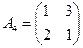матрицасымен берілген ойын шешімін табу керек.

Шешуі. 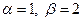; матрицаның егер нүктесі жоқ. (4.10)- (4.12) формулалары бойынша оптималды стратегияны және ойын бағасын табамыз.

.

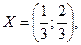
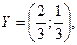
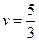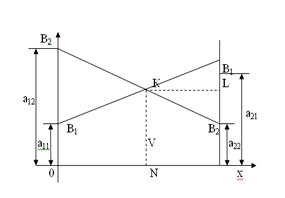
матрицасымен берілген ойын шешімін келесі құрылымдармен графикалық түрде табуға болады. Абцисса осіне ұзындығы 1-ге тең кесінді саламыз. Кесіндінің сол жағы (x=0 нүктесі) А₁ стратегиясына сай келеді, ал оң жағы – А₂ стратегиясы. х аралық нүктелері қандай да бір аралас (х₁, х₂) стратегияларға сай келеді, онда х₁=1-х, х₂=х. Таңдалған кесінді соңдарына абцисса остеріне перпендикуляр түзу жүргіземіз. Оған таза стратегия кезіндегі ұтыстарды қоямыз. Егер В ойыншысы В₁ стратегиясын қолданса, онда А₁ және А₂ таза стратегияларын қолданғандағы ұтыс сәйкесінше а₁₁ және а₂₁ –ге тең. Бұл нүктелерді түзу бойына орналастырамыз және алынған нүктелерді В₁В₁ түзуімен қосамыз. Егер А ойыншысы аралас стратегияны қолданса, онда оның ұтысына осы түзуде жататын (4.1. сурет) кейбір М нүктесі сай келеді.

В ойыншысының В₂ стратегиясына сәйкес В₂В₂ түзуін дәл осылай құрамыз (4.2 сурет). В₁KВ₂ қисығы – А ойыншысының алған

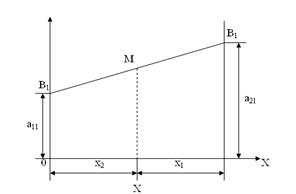
4.1 сурет 4.2 сурет

ұтыстарының төменгі шекарасы. K нүктесі ойын бағасын және оның шешімін анықтайды. В ойыншысы үшін оптималды стратегияны анықтау формуласы:

.

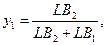
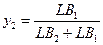Егер у₁ және у₂ анықтайтын формулаларға LB₂ және LВ₁ мәндерін қойсақ бұл қатынастың дұрыстығын байқауға болады. Онда мынаны аламыз:

LB₂ = v-a₂₂; LB₁ =a₂₁-v.

(4.11)-ден v- ні өрнектеп, (4.12)-ге сай келетін у₁ және у₂ мәндерін аламыз.

В ойыншысы үшін жоғарғы ұтыс шекарасының минималдау мәселесін қарастыруға болады. Ол үшін шешу барысында А және В ойыншыларының орнын ауыстыру керек.

Геометриялық түсіндірмені қолдап, өлшемді матрицамен берілген ойындардың шешімін табуға болады. В ойыншының n стратегияларының әрбіріне түзу сәйкес келеді. Бұл түзулерді тұрғызып, ұтыстың төменгі шекарасын табамыз. Төменгі шекарада жататын K нүктесі ойынның бағасы мен шешімін анықтайды. Ол үшін ұтыстын шамасы ең үлкен. В ойыншының белсенді стратегиялары анықталады (оларға сәйкес түзулер K нүктеде қиылысады).

Дәл солай матрицасы 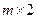өлшемді ойынды да шешуге болады, бірақ бұл жағдайда ұтыстың жоғары шекарасын құрып, онда минимумды табу керек.

Геометриялық құрылымдар ойыншылардың белсенді стратегиялар анықтау үшін қолданылады. Кейін ойынның шешімі (4.10)-(4.12)формулалар көмегімен табылады.

Мысал 3. Келесі матрицамен берілген ойынның шешімін табу керек:

.

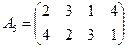Шешуі. 4.3 суреттегі түзулер В ойыншының стратегияларына, ал B₃KB₄ қисығы ұтыстың төменгі шекарасына сай келеді. В ойыншының тиімді стратегиялары– үшінші мен төртінші. (4.10)-(4.12) формулалар бойынша ойынның шешімін табамыз: 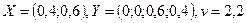. Демек, А ойыншысы А₁ стратегиясын 0,4 ықтималдықпен, ал А₂ стратегиясын – 0,6 ықтималдықпен қолдайды. Оның орташа ұтысы 2,2 бірлік болады.

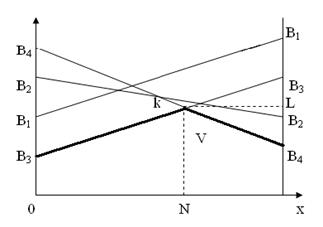
Сурет 4.3

Матрицалық ойындарды сызықтық программалау есебіне келтіру арқылы шешу әдістері

Өлшемі т ´ п болған А ойынды қарастыралық:

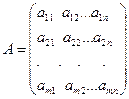
Матрицаның егер нүктесі жоқ, сондықтан ойын шешімі аралас стратегияларда ізделінеді: 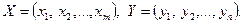. А ойыншы өзінің тиімді стратегиясын таңдағанда (7) шарт орындалады, ал (8) шарты В ойыншының тиімді стратегиясына қанағаттандырады. Сөйтіп, келесі шектеулер орындалатын А ойыншының тиімді стратегиясын табу есебін қарастыруға болады:

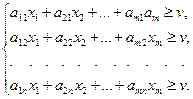(13)

v шамасы(ойынның бағасы) белгісіз, бірақ v > 0 санауға болады. Егер матрицаның элементтері теріс болмаса, соңғы шарт әрқашан орындалады. Кері жағдайда матрицаның барлық элементтеріне қандай да бір оң шаманы қосамыз.

Теңсіздіктердің барлық мүшелерін v- ға бөліп, шектеулер жүйесін түрлендіреміз. Нәтижеде

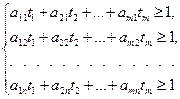(14)

аламыз, мұнда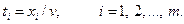

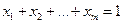шартынан

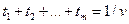(15)

шығады.

Ойынның шешімі v- нің мәнін максималдау керек, демек, 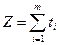функция минималды мәнін қабылдау керек. Сөйтіп, келесі сызықтық программалау есебі алынды:

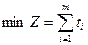
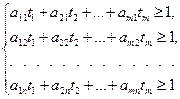(14)

.

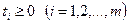Бұл есепті шешіп 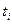мәнін және 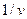шаманы, кейін 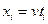мәндерді табамыз.

В ойыншының стратегиясын анықтау үшін келесі шарттарды жазамыз:

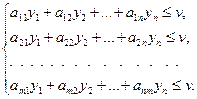(16)

Теңсіздіктердің барлық мүшелерін v- ға бөліміз:

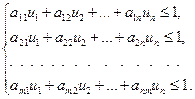(17)

Мұнда Переменные 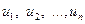айнымалыларды (17) шарттарды қанағаттандыратындай және

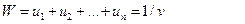(18)

функцияға максимум жеткізетіндей таңдау керек.

Сөйтіп, ойынды шешу үшін сызықты программалаудың қосалқы симметриялық есептердің жұбы бар.

Пәнді оқу-әдістемелік әдебиетпен әдістемелік қамтамасыз ету.

Негізгі әдебиеттер:

1. Айсағалиев С.Ә., Иманқұл Т.Ш. Тиімділеу әдістерінің дәрістері. «Қазақ университеті» баспасы, Алматы, 2004 ж.

2. Айсағалиев А.С., Айсағалиева С.С. Лекции по методам оптимизации. Изд-во «Наукаң», Алматы, 1996 г.

3. Габбасов Р.Ф., Кириллова Ф.Ф. Методы оптимизации. Минск, 1975.

4. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. М.: 1978 г.

5. Васильев Ф.П. Лекции по методам решения экстремальных задач. М.: 1974 г.

6. Карманов В.Г. Математическое программирование. М.: 1975 г.

7. Гельфанд И.М., Фомин С.В. Вариационное исчисление. М.: 1961 г.

8. Понтрягин Л.С. и др. Математическая теория оптимальных процессов. М.: 1976 г.

9. Гюнтер Н.М., Кузьмин Р.О. Сборник задач по высшей математике. М.:, Л., 1947 г., т.3, отд. 16.

10. Айсағалиев С.А., Бияров Т.Н., Калимолдаев М.Н., Мамытбеков Е.К. Задачи по методам оптимизации и вариационному исчислению. Алматы. 1996 г.

11. Таха Х. Введение в исследование операций. – М.: Изд.дом «Вильямс», 2001. – 912 с.

12. Вагнер Г. Основы исследования операций. – В 3-х томах. – Т.1, М.: Мир, 1972, 336 с. – Т.2, М.: Мир, 1973, 488 с. – Т.3, М.: Мир, 1973, 503 с.

13. Исследование операций / Под ред. Дж.Моулера, С.Элмаграби. – В 2-х томах. – Т.1 – М.: Мир, 1981. – 712 с.

14. Зайченко Ю.П. Исследование операций. – Киев: Выща школа, 1988. – 412 с.

Қосымша әдебиеттер:

1. Ройтенберг Я.Н. Автоматическое управление. М.; 1978 г.
2. Красовский Н.Н. Теория управления движением. Линейные системы. М.; 1968 г.
3. Болтянский В.Г. Математические методы оптимального управления. М.; 1969 г.
4. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. М.; 1965 г.
5. Алексеев В.М., Тихомиров В.Ф., Фомин С. Оптимальное управление. М.; 1979 г.