Сызықтық программалаудың транспорт есебі транспорт пен өнеркәсіп және өндірістің түрлі мәселелерінің теориялық зерттеулерінде және практикада жиі қолданылады. Әсіресе өнеркәсіп пен ауылшаруашылық өнімдерін жеткізуді рационализациялауда, сондай-ақ жүк айналымдарын оптималды жоспарлауда және транспорттың басқа да әртүрлі жұмыстарында ерекше маңызы бар.
3.1 Есептің қойылуы және оның математикалық моделі.
Барлығы m ұсынушыда, 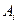 -де
-де 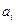 ,
, 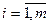 жинақталған біртекті заттарды, барлығы n тұтынушыға, Bj-ге bj,
жинақталған біртекті заттарды, барлығы n тұтынушыға, Bj-ге bj, 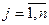 , жеткізу керек. Бірлік жүкті і–ұсынушыдан j- тұтынушыға тасымалдау бағасы Cij белгілі.
, жеткізу керек. Бірлік жүкті і–ұсынушыдан j- тұтынушыға тасымалдау бағасы Cij белгілі.
Тұтынушылар сұранысын толық қанағаттандыратын және бағасы минималды болатын, барлық жүкті тасымалдау жоспарын құру қажет.
і- ұсынушыдан j тұтынушыға тасымалдауға жоспарланған жүкті xij деп белгілеп, есептің шартын жоспарлау матрицасы аталатын кестемен жазуға болады.
| Ұсынушылар | Тұтынушылар | Қорлар | |||
| B1 | B2 | … | Bn | ||
| А1 | C11 x11 | c12 x12 | … | c1n x1n | a1 |
| А2 | C21 x21 | c22 x22 | … | c2n x2n | a2 |
| … | … | … | … | … | … |
| Аm | cm1 xm1 | cm2 xm2 | … | cmn xmn | am |
| Сұраныстар | b1 | B2 | … | bn | 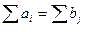 |
Есептің математикалық моделін құрайық.
і-ұсынушыдан j-тұтынушыға тасымалданатын жүк xij, оның тасымал бағасы 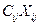 . Барлық жүкті тасымалдау бағасы
. Барлық жүкті тасымалдау бағасы
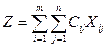
Шектеулер жүйесін есептің келесі шарттарынан аламыз:
1) барлық жүк тасымалдануы керек, яғни
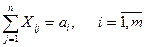
(бұл теңдеулер кестенің жолдарынан алынады).
2) сұраныстар түгелімен қанағаттандырылуы керек, яғни
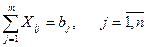
(бұл теңдеулер кестенің бағандарынан алынады).
Сонымен, транспорт есебінің математикалық моделі келесі түрде беріледі.
Сызықтық функцияның
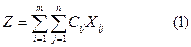
Ең кіші мәнін келесі шектеулерде
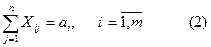
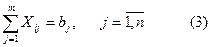
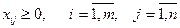
табу керек.
Қарастырып отырған модельде қорлар қосындысы сұраныстар қосындысына тең деп есептеледі, яғни
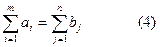
Бұндай модель тұйықталған (жабық) деп аталады.
Теорема. Қорларының қосындысы сұраныстарының қосындысына тең болатын кезкелген транспорт есебінің шешімі бар.
Теореманы дәлелдеу үшін, берілген шарттарда кемінде бір шешімі бар екендігін және сызықтық фукция шешімдер жиынында шектеулі екендігін көрсету қажет.
Дәлелдеуі.
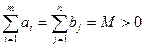 делік.
делік.
Онда
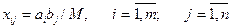
шамалары (2), (3) шектеулер жүйелерін қанағаттандыратындықтан, есептің шешімі болады. Шындығында да, xij мәндерін (2) және (3) – ке қойсақ табамыз.
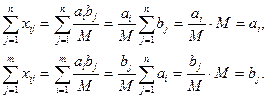
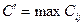 мәнін алып, сызықтық функцияны бағаласақ (2) тендік арқылы мынаны аламыз
мәнін алып, сызықтық функцияны бағаласақ (2) тендік арқылы мынаны аламыз
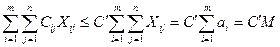
Дәл осы сияқты 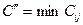 мәнін қолдансақ
мәнін қолдансақ
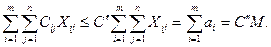
Соңғы екі теңсіздікті біріктіріп қарастырсақ 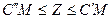 теңсіздігін аламыз, яғни сызықтық функция транспорт есебі шешімдерінің жиынында шектеулі.
теңсіздігін аламыз, яғни сызықтық функция транспорт есебі шешімдерінің жиынында шектеулі.
3.2 Бастапқы тірек шешімін құру.
Оптималдық шешімге бастапқы тірек шешімін құрумен жуықтайды.
Шектеулер жүйесінің (2)- (3) m,n белгісіздері, m+n теңдеулерімен берілген, сондай-ақ (4) қатынаспен байланысты.
Транспорт есебінің бастапқы тірек шешімін сызықтық программалау есебінің осыған дейінгі әдістері мен құруға болады, бірақ бұл үлкен есептеулерді керек етеді. Бастапқы тірек шешімін құрудың бірнеше жеңіл жолдары бар, соларды мысалдар арқылы қарастырамыз.
Солтүстік – батыс бұрыш әдісі.
Жүк бірінші тұтынушыға сұранысы орындалғанша түгелдей бірінші ұсынушыдан, жетпегені екіншісінен, ол да жетпесе үшіншісінен, т.с.с., жасалады.
Егер бірінші ұсынушының қоры сұраныстан артық болса, қалғаны екінші тұтынушыға, одан қалғаны үшіншіге, т.с.с. барлық қоры біткенше тасымалданады.
Қалған тұтынушылар мен ұсынушылар арасындағы тасымал да осы тізбекпен жалғасады. Тасымалдау тізбегі транспорт есебі кестесінің солтүстік - батыс бұрышынан басталып, оңтүстік – шығыс бұрышында аяқталады.
Мысал. Келесі есептің математикалық моделін және бастапқы тірек шешімін құру керек.
| Ұсынушылар | Тұтынушылар | Қорлар | |||
| В1 | В2 | В3 | В4 | ||
| А1 А2 А3 | |||||
| Сұраныстар |
Шешуі. Xij -i-ұсынушыдан j-тұтынушыға тасымал көлемі болсын. Барлық жүкті тасымалдау бағасы.
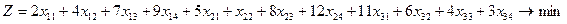 керек.
керек.
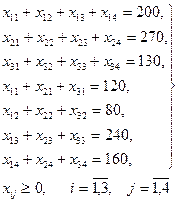
| Ұсынушылар | Тұтынушылар | Қорлар | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Сұраныстар |
Бірінші ұсынушының қоры 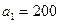 тұтынушының сұранысы
тұтынушының сұранысы 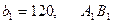 клеткасына 120 тасымалданып, бағанның басқа клеткалары сызылады, қалдық
клеткасына 120 тасымалданып, бағанның басқа клеткалары сызылады, қалдық 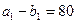 екінші тұтынушыға тасылады. Екінші тұтынушы сұранысы
екінші тұтынушыға тасылады. Екінші тұтынушы сұранысы 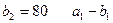 қалдығымен жабылады, сонымен
қалдығымен жабылады, сонымен 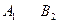 клеткасына 80 тасымалданып,
клеткасына 80 тасымалданып, 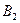 бағанының қалған клеткалары сызылады. Үшінші тұтынушының сұранысы
бағанының қалған клеткалары сызылады. Үшінші тұтынушының сұранысы 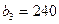 екінші ұсынушының қорынан
екінші ұсынушының қорынан 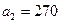 кем, сұраныс түгелімен орындалып, B3 бағанының қалған клеткалары сызылады, қалдық
кем, сұраныс түгелімен орындалып, B3 бағанының қалған клеткалары сызылады, қалдық 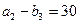 келесі сұранушыға B4 өтеді. Төртінші тұтынушының сұранысы үшінші A3 ұсынушының қоры a3=130 және
келесі сұранушыға B4 өтеді. Төртінші тұтынушының сұранысы үшінші A3 ұсынушының қоры a3=130 және 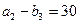 қалдығымен орындалады. Сонымен, барлық қорлар тұтынушылар талабына сай тасымалданды.
қалдығымен орындалады. Сонымен, барлық қорлар тұтынушылар талабына сай тасымалданды.
Құрылған тасымалдың жалпы құнын үлестері бар клеткалардың бұрыштарындағы сандар көбейтінділерінің қосындысынан аламыз.
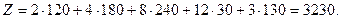
Кіші құн әдісі.
Кестедегі ең кіші құн жазылған (i,j) клеткасына ai,bj сандарының кішісі жазылып, қоры түгелдей тасылған ұсынушы жолы, немесе сұранысы түгелденген тұтынушы бағаны, немесе ai=bj болса жол да, баған да сызылады кестенің қалған бөлігінен тағы да кіші құн клеткасы таңдалып, жоғарыдағыдай әрекет қайталанады. Осылайша үлестіру барлық қорлар тасымалданып, сұраныстар түгелімен орындалғанша жалғасады.
Осы әдіспен бұған дейінгі есептің шешуін табайық. Есеп шартын кестеге жазып, барлық әрекетті орындасақ.
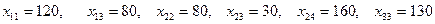
цикл құру мүмкін емес үлестіруін аламыз. Мұндағы m+n-1 саны үлестірулер санына тең, яғни құнарлы тірек шешімі алынғаны.
| Ұсынушылар | Тұтынушылар | Қорлар | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Сұраныстар |
тасымалдың жалпы құны.
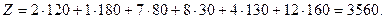
солтүстік – батыс бұрыш әдісімен алынған сандағыдан артық оптималдық шешіммен алшақтай түскен.
Қос мүмкіндік әдісі.
Әрбір бағанның ең кіші құн орналасқан клеткаларына V белгісі қойылып, дәл осылай белгілеу әрбір жолдың клеткаларына да қайталанады. Нәтижесінде қос VV белгісі бар клеткалар шығады. Тасымалдау әуелі қос VV белгілі клеткаларға, әрі қарай кіші құн әдісімен жасалады. Ұсынушы қоры түгесілсе – жол, тұтынушы сұранысы орындалса – баған сызылып отырады.
Жоғарыда келтірілген есепті қос мүмкіндік әдісі де қарастырайық.
| Ұсынушылар | Тұтынушылар | Қорлар | |||
| В1 | В2 | В3 | В4 | ||
| А1 | VV 2 | ||||
| А2 | VV 1 | ||||
| А3 | V 4 | VV 3 | |||
| Сұраныстар |
Алдымен 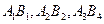 клеткаларын толтырамыз.
клеткаларын толтырамыз. 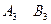 клеткасы түгесілген қорға байланысты A3 жолымен бірге сызылады. Кестенің қалған бөлігін кіші құн әдісімен толтырамыз:
клеткасы түгесілген қорға байланысты A3 жолымен бірге сызылады. Кестенің қалған бөлігін кіші құн әдісімен толтырамыз: 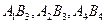 тасымалдау нәтижесінде
тасымалдау нәтижесінде
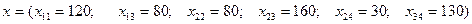
құнарлы тірек шешімін алдық. Оның құны
3.3 Потенциялдар әдісі
Теорема. Транспорт есебінің шешуі х*=(х*ij) оптималы болса, онда оған
U*i+V*j = Cij, егер Х*ij >0
және
 U*i+V*j = Cij , егер Х*ij = 0
U*i+V*j = Cij , егер Х*ij = 0
i =1,m; j =1,n
шарттарын қанағаттандыратын, барлығы m+n U*i және V*j сандарының жүйесі сәйкес. Сандар U*i және V*j тиісінше ұсынушылар және тұтынушылар потенциалдары деп аталады.
Дәлелдеуі.
Z = 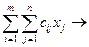 min
min

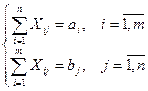
xij >=0, i= 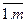 , j=
, j= 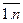 .
.
транспорт есебін сызықтық програмалаудың қайсыбір бастапқы, есебіне қосалқы деп қарастырсақ, онда бастапқы есебіне қосалқы деп қарастырсаң онда бастапқы
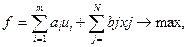
Ui +Vj <=>= c ij, i = 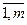 , j =
, j = 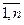 түрде беріледі.
түрде беріледі.
Х*-қосалқы есептің аптималды шешуді, сандықтан
Y*(Ui*, Vj*,), қосалқылық теоремасына сәйкес max f=min z
немесе
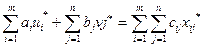 , хij*> =0
, хij*> =0
Берілген теоремаға сүйенген, қосалқы есептің аптималды шешуінің оң таңбалы компоненттеріне сәйкес бастапқы,,,,, шектеулі қатаң түрде өрнектеледі, яғни
U*+V*= C* ij, X*> 0,
U*+V*< = Cij X* =0.
Сонымен, бастапқы тірек шешімі аптималды болуы үшін, келесі шарттардың орындалуы қасиетті:
А),,,,, клетка үшін потенциалдар қосындысы тасмалдау бағытынан,,,керек, яғный
Ui +Vj<=Cij (**)
17, 18, 19, 20 – ші дәрістер. Дөңес бағдарламалау есептері
Мазмұны: Дөңес функциялар. Дөңес талдам элементтері. Локальды немесе глобальды минимум туралы. Глобал минимум туралы негізгі теорема
Келесі сызықтық емес бағдарламалау есебі қарастырылсын:
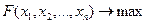 (1)
(1)
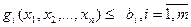 (2)
(2)
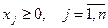 (3)
(3)
мұндағы F, gi – берілген функциялар.
Анықтама. Дөңес x жиынында берілген F (x) функциясы дөңес деп аталады, егер кез-келген x 1 және x 2 нүктелерімен кез-келген 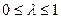 саны үшін келесі шарт орындалса:
саны үшін келесі шарт орындалса:
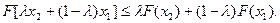 (4)
(4)
Анықтама. Дөңес x жиынында берілген F (x) функциясы дөңес деп аталады, егер кез-келген x 1 және x 2 нүктелерімен кез-келген 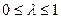 саны үшін келесі шарт орындалса:
саны үшін келесі шарт орындалса:
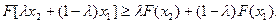 (5)
(5)
Анықтама. Дөңес бағдарламалау есебінің (1) – (3) Лагранж функциясы деп келесі функцияны айтады:
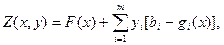 (6)
(6)
мұндағы 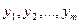 - Лагранж көбейтінділері.
- Лагранж көбейтінділері.
Анықтама. Лагранж функциясының ер нүктесі деп (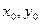 ) нүктесін айтады, егер барлық
) нүктесін айтады, егер барлық 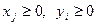 үшін келесі теңсіздіктер орындалса:
үшін келесі теңсіздіктер орындалса:
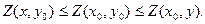 (7)
(7)
Теорема (Кун-Таккер). Берілген (1) - (3) дөңес бағдарламалау есебінің 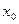 тиімді шешімі тек
тиімді шешімі тек 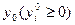 векторы болған жағдайда ғана болады; мұндағы (
векторы болған жағдайда ғана болады; мұндағы (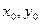 ) – Лагранж функциясының ер нүктесі болғанда:
) – Лагранж функциясының ер нүктесі болғанда:
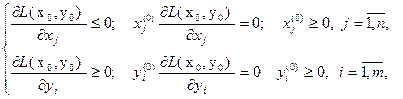 (8)
(8)
Сонымен, осы анықтамалар мен Кун-Таккер теоремасын пайдаланып, дөңес бағдарламалау есебін шешу жолын көрсетейік:
1. Лагранж функциясы құрастырылады.
2. Лагранж функциясы үшін (8) түрінде ер нүктесінің болуының қажеттілігі мен жеткілікті шарттары жазылады.
3. Ер нүктесінің болмауын анықтайды немесе ол нүктенің координатын табады.
4. Берілген есептің тиімді шешімін жазып, мақсат функциясының мәнін табады.
Осыған байланысты есептер қарастырайық.
Мысал. Келесі функцияның максимумын табуға
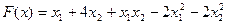
келесі шарттарды қолдану керек:
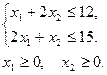
Шешуі.
1. Лагранж функциясын құрастыру:
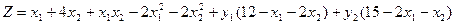 .
.
- (8) шарттарды пайдаланып:
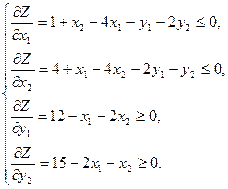 (9)
(9)
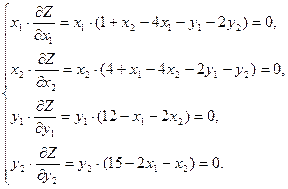 (10)
(10)
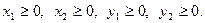 (11)
(11)
Сызықтық теңсіздіктерді (9) көшіріп жазайық:
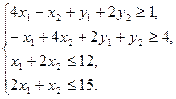 (12)
(12)
Қосымша айнымалы шамалар 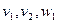 және
және 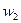 енгізу арқылы (12) орнына теңдеулер аламыз:
енгізу арқылы (12) орнына теңдеулер аламыз:
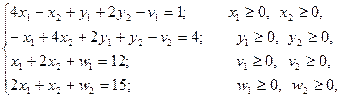 (13)
(13)
(10) мен (13) арқылы келесі теңдіктерді жазуға болады:
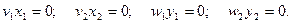
Егер (13) теңдеулер жүйесінің базистік шешімі табылса, онда Лагранж функциясының ер нүктесі немесе тиімді шешімі табылғаны.
3. Теңдеулер (13) жүйесінің базистік шешімдерін табу үшін жасанды базис әдісін пайдаланамыз. Ол үшін қосымша 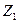 және
және 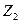 шамаларын енгізіп, келесі сызықтық бағдарламалау есебін қарастырамыз:
шамаларын енгізіп, келесі сызықтық бағдарламалау есебін қарастырамыз:
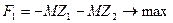
келесі шарттар:
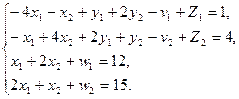
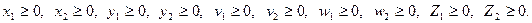
Бұл есептің шешуі келесі кестеде келтірілген:
| баз | 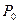 | - М | -М | ||||||||
 | 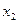 | 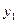 | 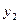 | 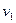 | 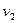 | 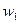 | 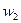 | 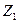 | 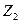 | ||
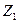 | -1 | -1 | |||||||||
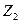 | -1 | -1 | |||||||||
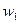 | |||||||||||
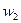 | |||||||||||
| -5 | -3 | -3 | -3 | ||||||||
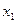 | 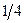 | 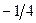 | 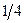 |  | 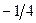 | 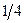 | |||||
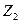 | 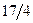 | 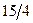 | 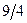 | 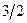 | 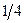 | -1 | 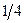 | ||||
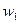 | 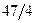 | 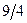 | 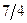 |  | 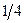 | 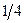 | |||||
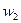 | 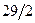 | 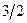 | 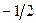 | -1 |  | 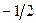 | |||||
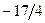 | 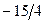 | 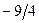 | 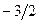 | 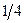 | 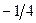 | ||||||
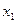 | 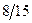 | 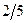 | 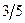 | 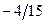 | 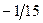 | 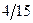 | 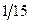 | ||||
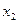 | 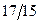 | 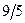 | 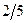 | 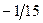 | 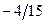 | 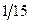 | 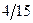 | ||||
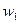 | 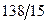 | 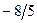 | 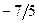 | 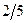 | 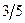 | 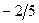 | 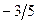 | ||||
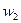 | 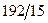 | 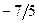 | 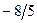 | 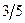 | 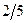 | 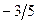 | 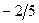 | ||||
Бұл кестеден:
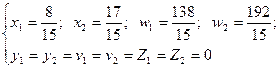
(10) формулаларынан:
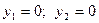
немесе
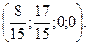
Нүктесі Лагранж функциясының ер нүктесі болады. Осыдан
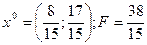
тиімді шешім болады.
Тақырыптың бақылау сұрақтары
1.Сызықтық программалау есептерінің мүмкін шешімдері қандай облыстарды құрайды?
2. Дөңес жиын дегеніміз не?
3. Тұйық жиын дегеніміз не?
4. Бұрыштық нүкте қандай болады?
5. Тіреуіш түзуін қалай тұрғызамыз?
6. Деңгей сызықтары дегеніміз не?
7. Шешімдер облысын қалай аламыз?
8. Максимум, минимум нүктелерін графиктік әдісте қалай анықтаймыз?
9. Шешімдер жиыны шектелмеген жиын(облыс) болса, есептің шешімі бола ма?
10. Шешімдер жиыны бос жиын болса, шешімі қандай болады?
21, 22 – ші дәрістер. Сызықтық емес бағдарламалау есебі
Мазмұны: Сызықтық емес программалау есебінің қойылуы. Тиімділіктің қажетті шарттары.
Сызықтық емес бағдарламалау есебін шешудің жалпы жүйесі. Графикалық
әдіс. Лагранж көбейткіштер әдісі. Лагранж функциясы.
Есептің қойылуы
Математикалық бағдарламалау есебінің жалпы түрін қарастырайық. Ол былайша қойылады:
мақсат функциясы
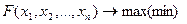 (1)
(1)
және шектеуші шарттар:
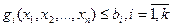 (2)
(2)
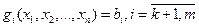 , (3)
, (3)
мұндағы F және g i – берілген функциялар, х j – айнымалы белгісіздер, ал b i – тұрақты шамалар. Берілген (2) және (3) шарттарын қанағаттандыратын және F функиясының максимумын (немесе минимумын) беретін белгісіздердің 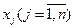 мәндерін табу керек.
мәндерін табу керек.
Егер F және барлық 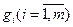 функциялары сызықтық болса, онда есеп жоғарыда қарастырылған сызықтық бағдарламалау есебі болады.
функциялары сызықтық болса, онда есеп жоғарыда қарастырылған сызықтық бағдарламалау есебі болады.
Шектеуші теңдеулер (3) мен теңсіздіктер (2) сызықтық емес болғандықтан бұл есептің анықталу облысы дөңес болмауы мүмкін және мақсат функциясының экстремум нүктелері анықталу облысының ішіндеде болуы мүмкін.
Сызықтық емес бағдарламалау есебін шешудің жалпы жүйесі.
Сызықтық емес бағдарламалау есебін шешу алгоритмі мынандай болады:
1. Алдымен есептің үйлесімді шешімдер облысын берілген шектемелер (2) және (3) арқылы анықтау керек.
2. Содан кейін кез-келген h санын гипербет тұрғызылады:
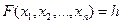 .
.
3. Осы гипербеттің ішінен h max(немесе h min) сәйкес болатын гипербет табылады; немесе F функциясының анықталу облысында шектелмегендігі анықталады.
4. Ең үлкен h max(немесе ең кіші h min)сәйкес келетін гипербет өтетін анықталу облысының нүктесі табылып, ондағы мақсат функциясының мәнін табу керек.
Графикалық әдіс.
Есептің шешу алгоритмі түсінікті болуы үшін алдымен графикалық әдісті қарастырайық.
Мысал. Келесі мақсат функциясының экстремумын берілген шектемелер 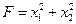 анықтайтын үйлесімді шешімдер облысынан табу керек.
анықтайтын үйлесімді шешімдер облысынан табу керек.
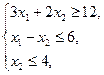
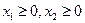 .
.
1. Берілген теңсіздіктер бойынша үйлесімді шешімдер облысын табамыз; ол ABCD төртбұрышы болады:
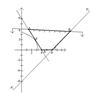
2. Егер F=h деп алсақ, онда 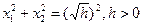
центрі 0(0, 0) нүктесіне орналаскан радиусы 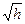 шеңбер алынады.
шеңбер алынады.
3. Әрине, үйлесімді шешімдер облысының 0 нүктесіне ең жақын орналасқан нүктесі үшін h ( немесе F) ең кіші мән қабылдайды; ал ең алыс орналасқан нүкте үшін ең үлкен мән қабылдайды.
4. 0 нүктесінен ең алыс нүкте бірден анықталады; ол В нүктесінің координаттары – келесі жүйені шешу арқылы табылады: 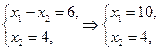
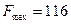 .
.
Ең жақын нүктені табу үшін 0 нүктесінен 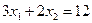 түзуіне дейінгі қашықтықты тапсақ жеткілікті:
түзуіне дейінгі қашықтықты тапсақ жеткілікті: 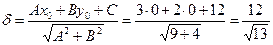 ,
,
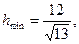
ал ол Е нүктеснің координаттары былайша табылады:
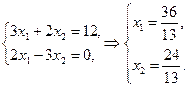
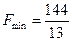 .
.
Сонымен, есептің шешуі: 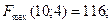
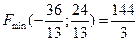
Лагранж көбейткіштер әдісі.
Сызықтық емес бағдарламалау есебінің жеке түрі ретінде шектемелері тек теңдеулерден тұратын жағдайын қарастырайық. Ол есепті классикалық тиімді есебі деп атайды:
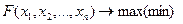 (4)
(4)
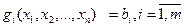 (5)
(5)
Бұл есепті шешу үшін Лагранж көбейткіщтер әдісін қолдануға болады. Ол бойынша 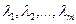 деген белгісіз айнымалыларды енгіземіз; олар Лагранж көбейткіштері деп аталады. Осыдан кейін Лагранж функциясы құрастырылады:
деген белгісіз айнымалыларды енгіземіз; олар Лагранж көбейткіштері деп аталады. Осыдан кейін Лагранж функциясы құрастырылады:
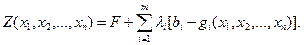 (6)
(6)
Осы Лагранж функциясының бірінші туындыларын нөлге теңестіру арқылы келесі теңдеулер жүйесін аламыз:
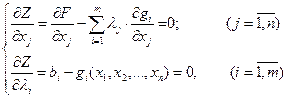 (7)
(7)
Бұл теңдеулер жүйесінің кез-келген шешімі F функциясының экстремумын береді.
Сонымен, Лагранж әдісінің шешу жолы былайша жазылады:
1. Лагранж функциясын (6) құрастыру.
2. Лагранж функциясының туындыларын тауып, оларды нөлге теңестіру керек.
3. Осыдан алынған (7) теңдеулер жүйесін шешу.
4. Осы шешімдердегі мақсат функциясының мәндерін тауып, салыстыру арқылы мақсат функциясының максимумын немесе минимумын анықтау.
Енді осы әдіске арналған мысал қарастырайық.
Мысал. 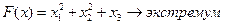
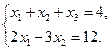
Шешуі:
1. Лагранж функциясын құрастырамыз:
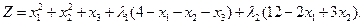
2. Лагранж функциясының туындыларын нөлге теңестіреміз: 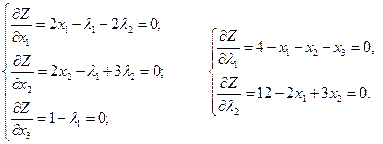
Осы теңдеулер жүйесінің шешуі: 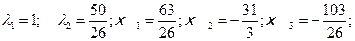
3. Мақсат функциясының осы шешімге сәйкес мәнін табамыз
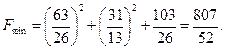
Тақырыптың бақылау сұрақтары
Сызықтық емес программалау есебінің қойылуы
- Сызықты емес программалау есебінде экстремум нүктесі мүмкін шешімдер жиыны облысының қай жерінде жатады?
- Егер есептің шектеулері сызықты емес болса, онда мүмкін
шешімдер облысы дөңес бола ма?
- Мүмкін шешімдер облысы дөңес болмаса, онда глобалды
оптимумнан басқа локалды оптимум нүктесі болуы мүмкін бе?
- Алынған оптимальды жоспар глобальды оптимум болуы үшін,
мүмкін шешімдер облысы және мақсат функция қандай болуы керек?
- Мүмкін шешімдер облысын қалай анықтаймыз?
- Лагранж көбейткіштер әдісінде шартты экстремумды анықтау үшін қандай функцияны құрамыз?
- Лагранж функциясы
- Лагранж көбейткіштер әдісі алгоритмі.
- Шартты экстремум дегеніміз не?
- Шартсыз экстремум түсінігін бер?
- Стационар нүктені қалай анықтаймыз?
- Глобальды минимум және максимумды қалай анықтаймыз?
- Шартты экстремум түсінігін білу.
- Дербес туындыны табу
- Шарт теңсіздік түрінде берілгенде Лагранж көбейткіштер әдісін қолдануға бола ма?
23, 24 – ші дәрістер. Бір айнымалылы функцияны минимумдау әдістері. Кесіндіні қақ бөлу әдісі. Алтын қима әдісі. Тиімді іздестіру. Сандық тізбектің қасиеті туралы лемма. Градиенттік әдіс. Градиент проекциясы туралы теорема. Ньютон әдісі. Лагранж көбейткіштері әдісі. Айыптық функциялар әдісі.
Сызықтық программалау есептер шешімдерінің қасиеттерін қарастырайық.
Жоғарыда айтылғандай сызықтық программалау есептерінің мүмкін жоспарлары есептің анықталу облысын құрайды.
Теорема: сызықтық программалау есептерінің анықталу облысы дөңес жиыннан құралады.
Анықтама 1. Егер жиынның екі кез келген нүктесі оларды қосатын түзу кесіндімен бірге жиынға енсе, онда жиын дөңес деп аталады.
Мысалы, (2.8) –(2.10) есептерінің жоспарларының көпшілігі дөңес болады, себебі шектеулер жүйесі АВСДЕ дөңес көпбұрышымен бейнеленген. Егер бұл жиынның кез келген екі нүктесін алатын болсақ, оларды қосатын кесінді де осы жиында жатады.
2.2. Суретте көрсетілген жиын дөңес емес.
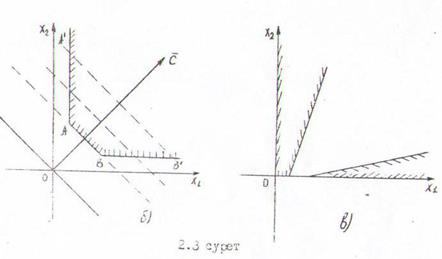
Анықтама 2. Егер жиынға барлық шекаралық нүктелер енсе, онда ол тұйық деп аталады.
Тұйық жиын (2.3 а) суретінде көрсетілгендей шектеулі және (2.3 б) суреттерінде көрсетілгендей шектеусіз болуы мүмкін.

Сызықтық программалау есептерінің мүмкін жоспарларының жиыны тұйық дөңес көпбұрыш құрайды. Көпбұрыштың төбелері бұрыштық нүктелері болып табылады. Түзу, жазықтық, жартылай жазықтық, кеңістік, жартылай кеңістіктің бұрыштық нүктелері болмайды.
Теорема (дәлелдеусіз). Сызықтық программалау есептерінің мақсатты функциясы өзінің экстремалды мәндерін шешімі болған көпбұрыштың бұрыштық нүктелерінде қабылдайды. Егер мақсатты функция эктремалды мәнін бірден көпбұрыштық нүктеде қабылдаса, онда сол мәнді ол нүктелерді қосатын кесіндінің кез келген нүктесінде қабылдайды.
Сызықтық программалу есептерінің жоспарлары:
1) Тұйықталып шектелген (2.3. а сурет) –бұл кезде бір немесе шексіз көп оптималды шешім қабылдайды;
2) Тұйықталған шектеусіз (2.3 б сурет) –бұл кезде бір немесе шексіз шешім қабылдайды немесе оптималды шешімі болмайды, себебі жиынның шектеусіздігіне сәйкес мақсатты функция да шектеусіз болады;
3) Бос (2.3 в сурет) –бұл жағдайда есептің қанағаттандыратын нүктелері болмайды.
Сонымен қатар сызықтық программалау есептерінің шешімі нүкте, кесінді, сәуле түрінде де берілуі мүмкін.
Ескерту. Сызықтық программалаудың нақты есептерінің әруақытта шешімі болады, яғни оптималды шешімі болады. Кейде есептің шартының дұрыс қойылмауы есептің шешілмеуіне әкеліп соғады.
Анықтама. Егер кез келген функция кесіндіден толығымен төмен (жоғары емес) жатса, кез келген екі нүктесін қосатын, барлық нүктелерінен, яғни егер кез келген х1 және х2 кез келген 0£ l £ 1 үшін болғанда функцияның мәндері х нүктесінде кесіндінің мәнінен артық емес 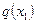 және
және 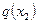 қосатын:
қосатын:
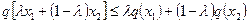 (1)
(1)
болса, онда 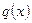 функциясы дөңес деп аталады.
функциясы дөңес деп аталады.
Анықтама. Егер де кесіндінің кез келген екі нүктесін қосатын:
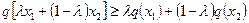 (1)
(1)
функциясы бар болса және ол кесіндіден толығымен жоғары (төмен емес) жатса, онда ол функция ойыс деп аталады.
 2015-05-14
2015-05-14 4550
4550








