Лабораторная работа 5 (2008 г.)
Рассмотрим решение систем линейных уравнений, заданных в матричном виде
А·X = B, где А – квадратная матрица коэффициентов левой части системы, В – вектор свободных членов. Вектор неизвестных находится как Х = В·А-1, где А-1 – обращенная матрица А.
Пример 1. Решим систему двух уравнений 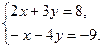
А= 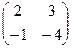 , В =
, В = 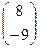 , Х =
, Х = 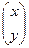
1 способ.
Находим обратную матрицу А-1.
А-1 = 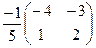 Используется команда Символика- Матрица – Инверсировать.
Используется команда Символика- Матрица – Инверсировать.
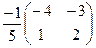 ·
· 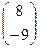 Используется команда Символика – Вычисление – Символически.
Используется команда Символика – Вычисление – Символически.
В результате получаем решение системы в виде 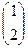
2 способ.
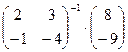 Используется команда Символика – Вычисление – Символически.
Используется команда Символика – Вычисление – Символически.
В результате получаем решение системы в виде 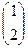
3 способ.
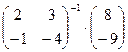 →
→ 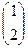
Пример 2. Решить систему трех уравнений: 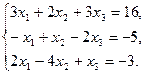
Решение: 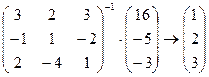 .
.
Пример 3.
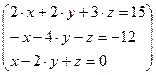 solve, x,y,z →
solve, x,y,z → 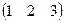
 2015-05-10
2015-05-10 191
191







