Линейная регрессия сущность, оценка параметров

Линейная регрессия сводится к построению уравнения вида y=a+b×x+ε

Построение уравнения регрессии сводится в первую очередь к расчету его параметров - а и b. Они могут быть определены разными методами. Наиболее распространенным методом, является метод наименьших квадратов (МНК).

Допустим, что заданы n наблюдаемых значений результативного признака (у) и признака-фактора (х).

Следует отметить, что рассчитываются не истинные значения a и b, а только оценки, которые могут быть хорошими или плохими.

Возникает вопрос: существует ли способ достаточно точной оценки а и b алгебраическим путем?

Вначале на поле корреляции построим точки соответствующие наблюдаемым значениям х и у и прямую, выражающую линейную регрессию (рис.2.2).

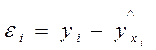Первым шагом является определение остатка для каждого наблюдения. Разность между фактическим и расчетным значением, соответствующим x_i, описывается как остаток в i-м приближении:

Рис.2.2 Точки рассеивания и прямая, выражающая линейную регрессию

Очевидно, что нужно построить такую линию регрессии, чтобы остатки были минимальными. Необходимо выбрать какой-то критерий подбора, который будет одновременно учитывать величину всех остатков.

Критерий минимизации суммы квадратов отклонений, фактических значений результативного признака (у) от расчетных (теоретических) :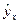

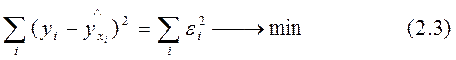заложен в основу МНК.

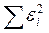
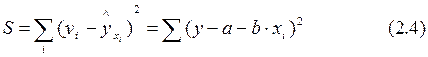Обозначим через S, тогда

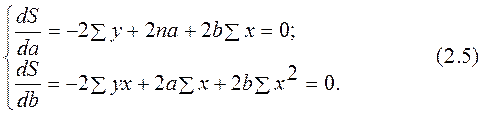Чтобы найти min (2.4), надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю:

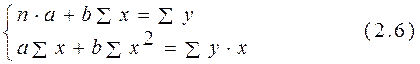Преобразуя систему (2.5), получаем следующую систему нормальных уравнений для оценки параметров a и b:

Решая систему (2.6), получим

,

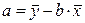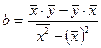, (2.7)

где ; ;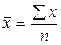

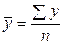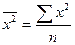
Параметр b называется коэффициентом регрессии. Его величина показывает, насколько единиц изменится результат с изменением фактора на одну единицу.

Параметр a, вообще говоря, не имеет экономической интерпретации. Например, если a <0, то попытка его экономической интерпретации приводят к абсурду.

Зато можно интерпретировать знак при параметре а. Если, а >0, то относительное изменение результата происходит медленнее, чем изменение фактора.