Функции нескольких переменных: определение, линии уровня

Пусть даны множества D 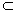R ⁿ и I 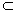R. Если каждой точке множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f (x ₁, …, x _n). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I.

Если зафиксировать любые n -1 переменные, то функция многих переменных превращается в функцию одной переменной. x ₂= с ₂, x ₃= с ₃, …, х _n= c _n; y=f (x ₁, c ₂, …, c _n) - функция одной переменной х ₁.

Пример. 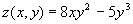- функция двух переменных,

- функция трех переменных.

Линией уровня функции двух переменных называется линия на плоскости XOY, принадлежащая D (z), в каждой точке которой функция принимает одно и то же значение.

Уравнение линии уровня: f(x, y) = c, где с - произвольное число. На данной линии уровня значение функции z=c. Линий уровня бесконечно много, и через каждую точку области определения можно провести линию уровня.

Частные производные функций нескольких переменных первого и второго порядка.

Частной производной от функции по независимой переменной называется производная

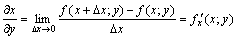, вычисленная при постоянном .

Частной производной по y называется производная , вычисленная при постоянном . Для частных производных справедливы обычные правила и формулы дифференцирования.