Хотя во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат, однако ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Так близость линейного коэффициента корреляции к нулю еще не значит, что связь между соответствующими экономическими переменными отсутствует. При слабой линейной связи может быть очень тесной, например, не линейная связь. Поэтому необходимо рассмотреть и нелинейные регрессии, построение и анализ которых имеют свою специфику.
В случае, когда между экономическими явлениями существует нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных эконометрических моделей.
Различает две группы нелинейных регрессионных моделей:
модели, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
модели нелинейные по оцениваемым параметрам.
К первой группе относятся, например, следующие виды функций:
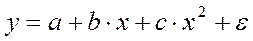 - полином 2-й степени;
- полином 2-й степени;
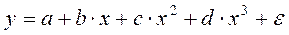 - полином 3-й степени;
- полином 3-й степени;
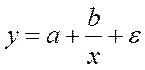 - гипербола.
- гипербола.
Ко второй группе относятся:
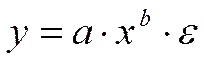 - степенная;
- степенная;
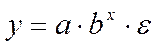 - показательная;
- показательная;
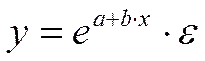 - экспоненциальная и др. виды функций.
- экспоненциальная и др. виды функций.
Классическим примером функций, относящихся к первой группе, являются кривые Филипса и Энгеля:
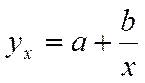 и
и 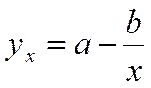 , соответственно.
, соответственно.
Первая функция характеризует нелинейные соотношения между нормой безработицы x и процентом прироста заработной платы у. Из данной зависимости следует, что с ростом уровня безработицы темпы роста заработной платы в пределе стремится к нулю.
Вторая функция устанавливает закономерность – с ростом дохода доля расходов на продовольствие - уменьшается. Здесь у, обозначает - долю расходов на непродовольственные товары; х – доходы.
Первая группа нелинейных функций легко может быть линеаризована (приведены к линейному виду). Например, для полинома к -го порядка
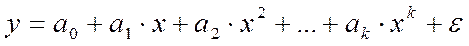 производя замену:
производя замену:
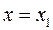 ,
, 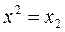 ,
, 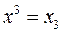 ,…,
,…, 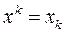
получим линейную модель вида
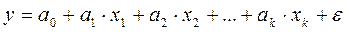 .
.
Аналогично могут быть линеаризованы и другие виды нелинейных функций 1-й группы, производя соответствующие замены.
Для оценки параметров нелинейных функций первой группы можно использовать, обычный МНК, аналогично, как и в случае линейных функций.
Иначе обстоит дело с группой регрессионных, нелинейных функций по оцениваемым параметрам. Данную группу функций можно разбить на две подгруппы:
нелинейные модели внутренне линейные;
нелинейные модели внутренне нелинейные.
Рассмотрим степенную функцию  . Она нелинейна относительно параметров
. Она нелинейна относительно параметров 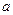 и b. Однако ее можно считать внутренне линейной, так как, прологарифмировав ее можно привести к линейному виду:
и b. Однако ее можно считать внутренне линейной, так как, прологарифмировав ее можно привести к линейному виду:
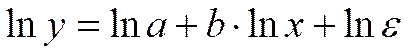 .
.
Следовательно, ее параметры могут быть найдены обычным МНК.
Если модель представить в виде:
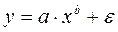 , то модель становится внутренне нелинейной, т.к. ее невозможно преобразовать в линейный вид.
, то модель становится внутренне нелинейной, т.к. ее невозможно преобразовать в линейный вид.
Внутренне нелинейной будет и модель вида
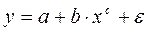
В эконометрических исследованиях, часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые легко преобразуются в линейный вид, относятся к группе линейных моделей. Например, к линейным относят модель:
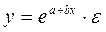 , так как
, так как
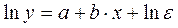 .
.
Если, модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные методы, успешность которых зависит от вида функции и особенностей применяемого итеративного подхода.
МНК в случае нелинейных функций, рассмотрим на примере оценки параметров степенной функции  .
.
Прологарифмировав данную функцию, получим:
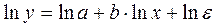 или, производя обозначения:
или, производя обозначения:
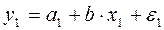 , где
, где
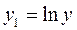 ;
; 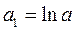 ;
; 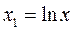 ;
; 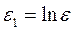 .
.
Применив МНК к полученному уравнению:
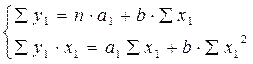 , или
, или
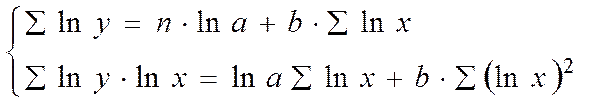
Параметр b определяется непосредственно из системы, а параметр а – косвенным путем: 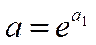
 2015-05-18
2015-05-18 465
465








