Степенная модель

Уравнение степенной модели имеет вид:

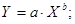
Для нашего примера:

Y – Валовый доход растениеводства, приходящийся на 100 га пашни, тыс. руб. (результативный признак);

Х – Доля трактористов – машинистов в общей численности работников, занятых в сельскохозяйственном производстве, % (факторный признак).

Данная функция нелинейна относительно параметров, но линейна по переменным. Прежде, чем проводить анализ необходимо перейти от нелинейной формы к линейной. В нелинейных регрессиях относительно параметров процедура лианеризации (аноморфоза) производится путем логарифмирования обеих частей уравнения:

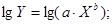
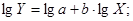
Введем замену:

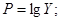
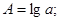
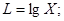
Вновь полученное уравнение будет иметь вид: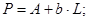

Таблица 9. Расчетные величины, необходимые для определения параметров уравнения

№ хозяйства	Доля трактористов-машинистов в общей численности работников, занятых в сельскохозяйственном производстве, % X	Валовый доход растениеводства, приходящийся на 100 га пашни, тыс.руб. Y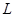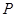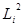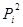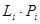
	34,0426	48,2162	1,532023	1,683193	2,347094	2,833139	2,57869
	24,1935	46,3568	1,383699	1,666113	1,914622	2,775934	2,305399
	28,2486	47,4703	1,450997	1,676422	2,105392	2,810391	2,432483
	18,9850	40,5136	1,278411	1,607601	1,634334	2,58438	2,055174
	27,1845	100,7356	1,434321	2,003183	2,057278	4,012742	2,873208
	11,9266	59,4603	1,076517	1,774227	1,158888	3,147882	1,909985
	19,5652	61,4004	1,291484	1,788171	1,667932	3,197556	2,309395
	18,1208	49,7596	1,282806	1,861969	1,64559	3,466929	2,388544
	15,8228	99,1870	1,258177	1,696877	1,58301	2,879391	2,134972
	19,1781	72,7728	1,199283	1,996455	1,438281	3,985832	2,394315
	35,7143	47,1492	1,552842	1,673474	2,411319	2,800516	2,598641
	252,9819	673,0219	14,7406	19,4277	19,9637	34,4947	25,9808
сред.знач.	22,9984	61,1838	1,34005	1,76615	1,81489	3,13588	2,36189
Среднее квадратич отклонение	7,2018853	20,173584

Найдем среднее квадратическое отклонение по L:

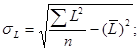
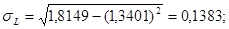
Для расчета параметров уравнения регрессии воспользуемся готовыми формулами:

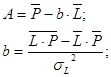
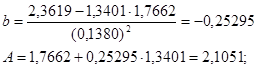
Уравнение принимает вид: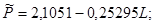

Проведем потенцирование полученного уравнения:

A=Lg a = 2.1051

a= 10^2.1051

b= -0.25295

lgY = 10^2.1051*(-0.25295)lgX

Y=127.3836*X^-0.25295

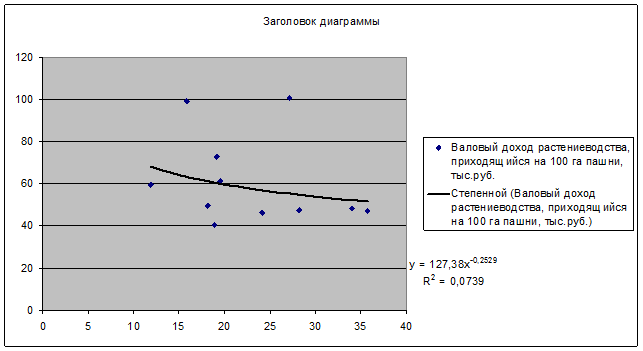
Рис. 4. Влияние доли трактористов – машинистов в общей численности работников, занятых в сельскохозяйственном производстве, на валовый доход растениеводства, приходящийся на 100 га пашни.

Коэффициент эластичности рассчитывается по формуле:

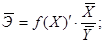
В нашем случае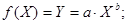

И формула коэффициента эластичности парной линейной регрессии принимает вид:

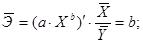
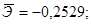
С увеличением доли трактористов – машинистов в общей численности работников, занятых в сельскохозяйственном производстве, на 1 % валовый доход растениеводства, приходящийся на 100 га пашни, уменьшается в среднем на 0,2617%.

Для нелинейной парной корреляции рассчитывается индекс корреляции:

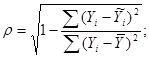
Для расчета индекса корреляции выполним вспомогательные расчеты (таблица 10).

Таблица 10. Расчетные величины, необходимые для расчета индекса корреляции и определения показателей аппроксимации

№ хозяйства	Доля тракторис-тов-машинистов в общей численности работников, занятых в сельскохозяйственном производстве, %	Валовый доход растениеводства, приходящийся на 100 га пашни, тыс.руб.	Расчетные величины
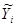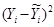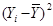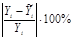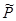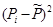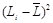	34,0426	48,2162	52,190896	15,79820936	168,1586498	8,243486908	1,717595	0,0012	0,036853
	24,1935	46,3568	56,900057	111,1602591	219,839929	22,74371089	1,755113	0,0079	0,001905
	28,2486	47,4703	54,71292	52,45554041	188,0600823	15,2571602	1,73809	0,0038	0,012309
	18,9850	40,5136	60,498539	399,3977771	427,257168	49,32896301	1,781745	0,0303	0,0038
	27,1845	100,7356	55,246899	2069,221877	1564,344883	45,15652912	1,742308	0,0681	0,008887
	11,9266	59,4603	68,047648	73,74254765	2,97045225	14,44215403	1,832813	0,0034	0,06945
	19,5652	61,4004	60,039622	1,85171669	0,04691556	2,216236331	1,778438	0,0001	0,002359
	18,1208	49,7596	60,343875	154,4781809	134,304921	17,0790806	1,780633	0,0066	0,003277
	15,8228	99,1870	61,215697	131,2421549	130,5123456	23,02288773	1,786863	0,0081	0,006703
	19,1781	72,7728	63,351922	1284,152795	1444,24321	36,1288049	1,80176	0,0379	0,019816
	35,7143	47,1492	51,561859	19,47156064	196,9699972	9,358926842	1,712329	0,0015	0,04528
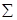	252,9819	673,0219	644,1099	4312,97262	4476,708554	242,97794	19,4277	0,1689	0,21064
сред. знач.	22,9984	61,1838	-	-	-	22,0889

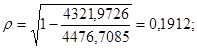
Индекс корреляции показывает, что между долей трактористов – машинистов в общей численности работников, занятых в сельскохозяйственном производстве, и валовым доходом растениеводства, приходящийся на 100 га пашни, слабая.

Коэффициент детерминации для нелинейных функций рассчитывается по формуле:

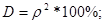
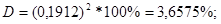
Следовательно, вариация валового дохода растениеводства, приходящийся на 100 га пашни, на 3,6575% объясняется вариацией доли трактористов – машинистов в общей численности работников, занятых в сельскохозяйственном производстве, а остальные 96,3425% вариации валового дохода растениеводства, приходящийся на 100 га пашни, обусловлены изменением других, не учтенных в модели факторов.

Оценим модель через среднюю ошибку аппроксимации:

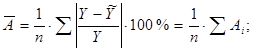
Средняя ошибка аппроксимации равна 22,0889%, т.е. в среднем расчетные значения валового дохода растениеводства, приходящийся на 100 га пашни, отличаются от фактических на 22,0889%, что не входит в допустимый предел. Данная модель имеет наименьшую ошибку аппроксимации.

Оценим модель через F-критерий Фишера. F-критерий Фишера необходим для проверки нулевой гипотезы о статистической незначимости уравнения регрессии и показателя тесноты связи.

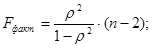
Выдвинем H₀ о статистической незначимости полученного уравнения регрессии и показателя тесноты связи.

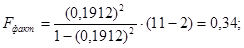
Сравним фактическое значение F-критерия с табличным. Для этого выпишем из таблицы «Значения F-Фишера при уровне значимости α=0,05» табличное значение.

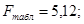
Так как F_факт<F_табл,то при заданном уровне вероятности α=0,05 следует принять нулевую гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента.

Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки:

; ;

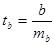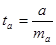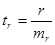
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

;

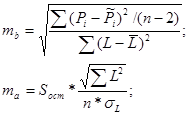
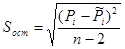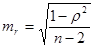
Выдвинем нулевую гипотезу о незначимости коэффициентов корреляции и регрессии.

Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции:

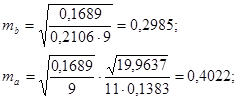
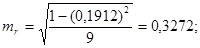
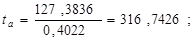
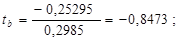
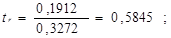
t_табл при уровне значимости α=0,05 и числе степеней свободы, равном 9, равно 2,2622.

Так как | t_b| <t_табл и t_r <t_табл, следовательно, Н₀ о незначимости коэффициентов корреляции и регрессии подтверждается.

Взаимосвязь между t-статистикой и F-статистикой:

;

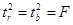
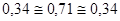8. прогноз значения результативного признака при прогнозном значении факторного, составляющем 125% от его среднего уровня (т.е. 125% от ).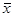

В виду того, что все уравнения регрессии являются статистически незначимыми, рассчитывать прогнозируемое значение валового дохода растениеводства, приходящегося а 100 га пашни ни по одному из рассмотренных уравнений не имеет смысла, поскольку данный прогноз не даст достоверного результата.

Тем не менее, для закрепления методики расчета прогнозов, выполним расчет прогнозного значения результата по степенной модели, так как в данном случае средняя ошибка аппроксимации минимальна.

Расчет прогнозного значения будем производить по линейной модели, так как значение квадрата индекса корреляции (R²) для нее максимальное

№ п/п	Модель	Средняя ошибка аппроксимации	R2 (ρ2)
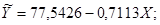		24,33	0,064
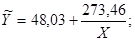		25,104	0,045
	Y=127.3836*X-0.25295	22,0889	0,037

По условию задачи прогнозное значение фактора составляет 125% от его среднего уровня 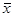=22,9984:

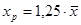=1,25∙22,9984=28,7479

и прогнозное значение среднедушевого прожиточного минимума в день при этом составит:

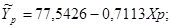
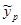= 77,5426-0,7113*28,7479= 57,0942

Если доля машинистов-трактористов составит 125% от среднего уровня 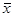=22,9984, то валовой доход растениеводства, приходящийся на 100 га пашни составит 57,0942 тыс. руб.