2015-05-18
811
Одним из предположений классической регрессионной модели является то, что случайные ошибки некоррелированы между собой и имеют постоянную дисперсию. В тех случаях, когда наблюдаемые объекты достаточно однородны, не слишком отличаются друг от друга, такое допущение оправдано. Однако во многих ситуациях такое предположение нереалистично. Это означает, что дисперсии зависимых величин не постоянны. Это явление в эконометрике называется гетероскедастичностъю (в отличие от гомоскедастичности – равенства дисперсий). Кроме того, при анализе временных рядов в довольно редких случаях можно считать, что наблюдения некоррелированы во времени. Как правило, значение исследуемой величины в текущий момент времени статистически зависит от ее значений в прошлом, что означает наличие корреляции между ошибками. Поэтому естественно изучать модели регрессии без предположения, что V(e) = s2 I.
Рассмотрим так называемую обобщенную регрессионную модель
у = Хb + ε,(9.5)
где у – n х 1 вектор зависимой переменной;
|
|
|
X – n x kматрица независимых переменных;
B – k x 1 вектор неизвестных параметров;
ε – n x 1 вектор случайных ошибок, причем:
1) матрица X неслучайна и имеет полный ранг;
2) Е(ε) = 0;
3) V(ε) =W и матрица W положительно определена.
Обычный метод наименьших квадратов давал оценку для коэффициента регрессии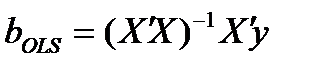 
, но в данном случае оценки могут быть смещенными. Применяя обобщенный метод квадратов, можно получить следующее выражение
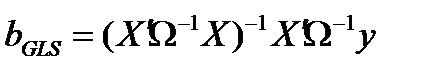. (9.6)
Для применения ОМНК необходимо знать матрицу W, что на практике бывает крайне редко. Поэтому вполне естественным кажется такой способ: оценить (каким-нибудь образом) матрицу W, а затем использовать эту оценку вместо W. Этот подход составляет суть так называемого обобщенного метода наименьших квадратов
21. Использование статистик для определения значимости оценок параметров (уравнения регрессии).
Для оценки качества уравнения в целом используется F-критерия Фишера
Сопоставляя факторную (RSS) и остаточную (ESS) дисперсии в расчете на одну степень свобод, получим величину F-критерия: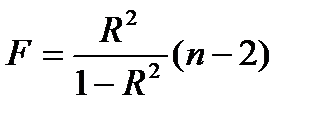 
Степень свободы:
n-2 остаточной(ESS), парной регреcсии
n-p, n– количество наблюдений, объем выборки.
P– количество определяемых факторов.
Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы.
Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи.(или обратно)
|
|
|
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: mb и ma.
; 
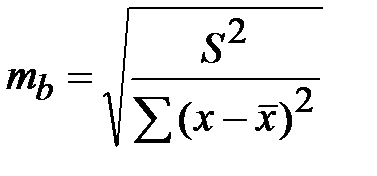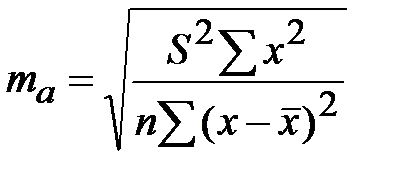(8.4)
где S2 - остаточная дисперсия на одну степень свободы
Величина стандартной ошибки совместно с t-распределением Стьюдента при n -2 степенях свободы применяется для проверки существенности коэффициента регрессии.
При гипотезе Н0 : b-b0 =0, t-статистика выглядит следующим образом:
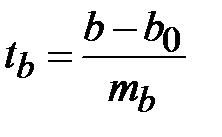
Наиболее просто t-статистика выглядит при гипотезе Н0 : b =0. Это значение и приводится всеми компьютерными пакетами в результатах регрессии. В этом случае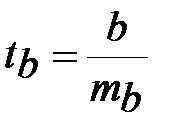 
.
Значение │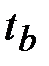 
│ сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n -2).
Если фактическое значение t-критерия превышает табличное, то гипотезу о несущественности коэффициента регрессии можно отклонить
