2015-05-18
638
Конечной целью статистического анализа временных рядов является прогнозирование будущих значений исследуемого показателя. Различают д/ср и кр/ср прогнозирование. В первом анализируется долговременная динамика исследуемого процесса, и главным считается выделение общего направления его изменения (тренда). Для предсказания кр/ср колебаний проводится более детальный регрессионный анализ с целью выявления большого числа показателей, определяющих поведение исследуемой величины.
Пусть оценивается модель вида Y^t = b0+b1*xt в момент времени (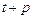
). Значение Y^t+p – значение по уравнению регрессии, построенному по МНК. Тогда доверительный интервал для действительного значения 
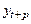множественной регрессии имеет вид:
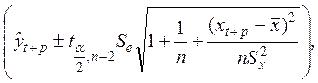
где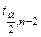 
– критическое значение, определяемое для соответствующего уровня значимости 
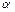и числа степеней свободы 
; 
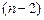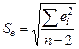– стандартная ошибка оценки (стандартная ошибка регрессии); 
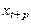– значение объясняющей переменной в момент (); 
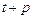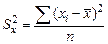– дисперсия переменной 
.
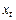После получения прогнозных значений необходимо проверить качество прогноза. Для этого используются следующие показатели:
· Относительная ошибка прогноза, вычисляемая по формуле:
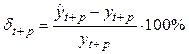или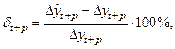 
Чем больше значение ошибки (выраженное в процентах), тем хуже качество прогноза.
· Стандартная среднеквадратическая ошибка, рассчитываемая по формуле: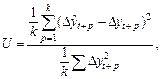 
где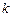 
– количество прогнозных периодов.
Значения показателя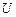 
лежат в интервале от нуля до единицы.
При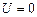 
прогноз абсолютно точен. Таким образом, чем ближе значение 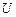к нулю, тем точнее прогноз.
· Точечный прогноз осуществляется путем подстановки требуемого значения в полученное уравнение регрессии.
Интервальная оценка для линейной парной регрессии находится из условия:
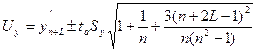
где L - период упреждения;
уn+L - точечный прогноз по модели на (n + L)-й момент времени;
n - количество наблюдений во временном ряду;
Sy -стандартная ошибка прогнозируемого показателя, рассчитанная по ранее приведенной формуле;
ta - табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
