Алгоритм проверки значимости регрессора в парной регрессионной модели. 25

Рассмотрим уравнение парной регрессии

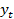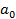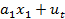= + (6.3)

Предполагается, что выполняются предпосылки теоремы Гаусса-Маркова.

Запишем модель 6.3 в следующем виде: 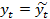+ 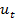(6.4)

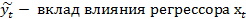
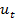- вклад влияния случайных факторов, не связанных с регрессором

Отсюда вытекает идея тестирования: необходимо установить, какое из слагаемых вносит больший вклад в общий разброс наблюдаемых значений эндогенной переменной.

Характеристикой разброса случайной переменной служит дисперсия, следовательно, необходимо определить какое из слагаемых преобладает в функции дисперсии эндогенной переменной.

Найдем дисперсию функции (6.4)

Таким образом

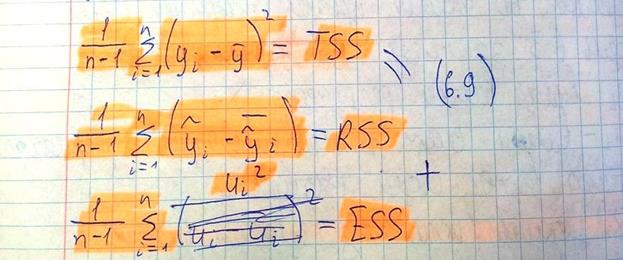
В качестве меры влияния регрессора на формирование значения эндогенной переменной вводится коэффициент детерминации 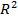= 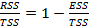, где RSS – регрессионная сумма квадратов, TSS – общая сумма квадратов, ESS – ошибка.

Если 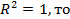RSS=TSS, ESS=0, следовательно, на эндогенную переменную влияют только регрессоры (идеальная ситуация)

Если 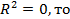ESS =TSS, RSS =0, следовательно, на эндогенную переменную влияют только случайные возмущения.

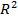показывает, какая доля изменения зависимой переменной обусловлена изменением объясняющей переменной. Коэффициент детерминации показывает процент влияния регрессора на эндогенную переменную.