Тестирование отсутствия автокорреляции случайного остатка

Проверяется третья предпосылка теоремы Гаусса-Маркова, которая говорит о независимости случайных переменных в уравнениях наблюдений, т.е.ковариация между случайными переменными равна 0: Cov(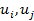)=0 i,j = 1,2,3…,n; i 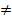j

Невыполнение третьей предпосылки теоремы Гаусса – Маркова, или наличие взаимосвязи случайных переменных в модели называется автокорреляцией.

Для тестирования автокорреляции в регрессионных моделях наиболее часто применяется тест Дорбина-Уотсона (DW).

Рассмотрим случай взаимного влияния случайных возмущений в соседних наблюдениях (текущ., предшеств.).

В основе теста лежат следующие предпосылки:

1) случайные возмущения подчиняются нормальному закону распределения

2) случайные возмущения подчиняются следующему правилу

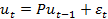
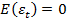
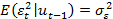(гомоскедастичный остаток)

Статистика DW, c помощью которой тестируется модель на автокорреляцию, имеет вид:

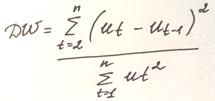где t-номер наблюдения, n-количество наблюдений

Найдем область определения статистики DW: (раскроем квадрат разности в числителе)

Таким образом, критическое значение статистика DW зависит не только от значения доверительной вероятности, количества регрессоров в модели и числа наблюдений, но еще и от абсолютных значений регрессоров.

Данное обстоятельство не дает получить единое значение для любой выборки (модели) критическое значение .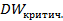

В каждом конкретном случае необходимо искать свое 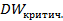, что неудобно.

Выяснилось, что можно найти отрезок [ 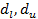], внутри которого находятся все возможные значения 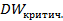. Тогда для принятия решения относительно наличия или отсутствия автокорреляции предлагается следующая схема DW:

1) строится отрезок [0;4], на котором отмечаются значения ;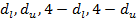

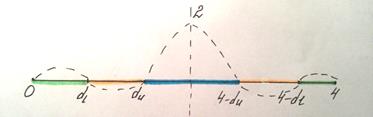
2) Возможны следующие варианты (куда попадает реальное значение DW):

а) если реальное значение DW попало в отрезки от [ 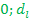] и [ 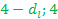], то автокорреляция существует (что плохо, т.к. случайные переменные влияют друг на друга) и гипотеза об отсутствии автокорреляции отклоняется)

б) если DW попало в отрезок [ 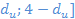,то автокорреляции нет, т.е. гипотеза принимается

в) если реальное значение DW находится в отрезках [ 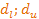] и [ 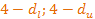], то невозможно сказать есть или нет автокорреляция, т.е. значение DW попало в зону неопределенности (единств.способ раскрыть неопределенность воспользоваться другой выборкой, в качестве измененной выборки может служить исходная с измененной последовательностью наблюдений).

Алгоритм теста DW:

Шаг 1. по результатам наблюдений оценить модель линейной регрессии

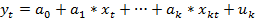
Шаг 2. для каждого оцененного уравнения, рассчитывается (оценивается) случайные возмущения

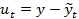
Шаг 3. по соответствующим статистическим таблицам находим значени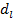и и 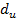, через k и n (доверит.вероятность 0,95)

Шаг 4. Проверяем в какой интервал на отрезке попал DW.