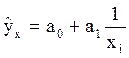Соотношение между социально-экономическими явлениями и процессами не всегда можно выразить линейными функциями. Так, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства — трудом, капиталом и т.д.), функции спроса (зависимость между спросом на товары, услуги и их ценами или доходом) и др.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Нелинейность может проявляться как относительно переменных, так и относительно входящих в функцию коэффициентов (параметров).
Различают два класса нелинейных регрессий:
Ø регрессии, нелинейные по переменным, включенным в анализ, но линейные по оцениваемым параметрам (различные полиномы, гипербола, полулогарифмическая функция)
Ø регрессии, нелинейные по оцениваемым параметрам (степенная, показательная, экспоненциальная функции)
Для оценки параметров нелинейных моделей используют два метода.
Первый метод основан на линеаризации модели и заключается и том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.
Второй подход обычно применяют в случаях, когда подобрать соответствующее линеаризующее преобразование не удается. Тогда используют методы нелинейной оптимизации на основе исходных переменных.
Чаще всего в эконометрических расчетах применяют следующие виды нелинейных регрессий: полином второго порядка, гипербола, степенная функция и показательная функция.
Оценка параметров нелинейной регрессии по переменным, включенным в анализ, но линейным по оцениваемым параметрам, проводится с помощью МНК путем решения нормальных уравнений.
Ø Регрессии, нелинейные по переменным, но линейные по оцениваемым параметрам:
- наименование регрессии: полином второго порядка
нормальные уравнения 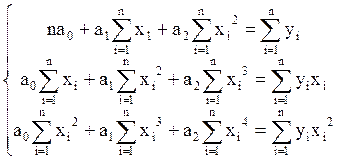
- наименование регрессии: гипербола
нормальные уравнения 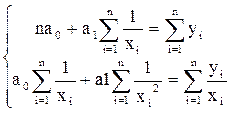
При замене в уравнениях 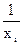 новой переменной X получают линейное уравнение
новой переменной X получают линейное уравнение 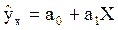
параметры модели определяют по формулам:
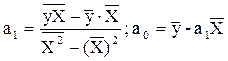
Ø Линеаризация регрессий, нелинейных по оцениваемым параметрам
- наименование регрессии: степенная функция
уравнение регрессии 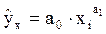
Для определения параметров степенной функции с помощью МНК необходимо привести ее к линейному виду путем логарифмирования обеих частей уравнения: 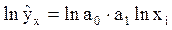 Это уравнение представляет собой прямую линию на графике, по осям которого откладываются не сами числа, а их логарифмы (так называемая логарифмическая шкала или логарифмическая сетка). Пусть
Это уравнение представляет собой прямую линию на графике, по осям которого откладываются не сами числа, а их логарифмы (так называемая логарифмическая шкала или логарифмическая сетка). Пусть 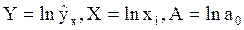 . Тогда уравнение примет вид
. Тогда уравнение примет вид 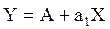 .
.
параметры модели определяют по формулам:
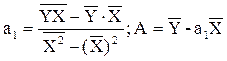
- наименование регрессии: показательная функция
уравнение регрессии 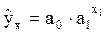
Линеаризацию переменных проводят путем логарифмирования обеих частей уравнения: 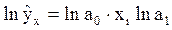 . Уравнение изображается прямой линией на полулогарифмической сетке, которая получается как сочетание натуральной шкалы для значений независимой переменной х и логарифмической шкалы — для значений зависимой переменной у. Пусть
. Уравнение изображается прямой линией на полулогарифмической сетке, которая получается как сочетание натуральной шкалы для значений независимой переменной х и логарифмической шкалы — для значений зависимой переменной у. Пусть 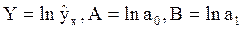 . Тогда уравнение примет вид
. Тогда уравнение примет вид 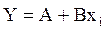 .
.
параметры модели определяют по формулам:
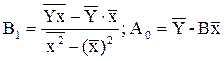
При использовании любой формы криволинейной корреляционной зависимости теснота связи между переменными может быть измерена с помощью индекса корреляции, который определяется аналогично коэффициенту корреляции для линейной формы связи.
Уравнение корреляционной связи должно быть по возможности более простым, чтобы сущность изучаемой зависимости между переменными проявлялась достаточно четко, а параметры уравнения поддавались определенному экономическому толкованию. Вопрос выбора соответствующего уравнения связи решается в каждом случае отдельно.
Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:
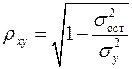 , где
, где
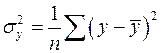 – общая дисперсия результативного признака
– общая дисперсия результативного признака 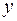 ,
, 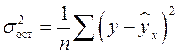 – остаточная дисперсия.
– остаточная дисперсия.
Уравнение для расчета индекса корреляции может иметь вид 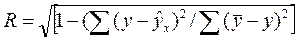
Величина данного показателя находится в пределах: 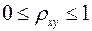 . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака 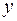 , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака:
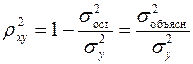 , т.е. имеет тот же смысл, что и в линейной регрессии;
, т.е. имеет тот же смысл, что и в линейной регрессии;
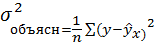
Индекс детерминации 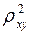 можно сравнивать с коэффициентом детерминации
можно сравнивать с коэффициентом детерминации 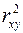 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина 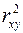 меньше
меньше 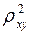 . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.
. А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.
Индекс детерминации используется для проверки существенности в целом уравнения регрессии по 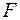 - критерию Фишера:
- критерию Фишера:
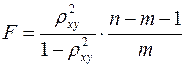 ,где
,где
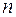 – число наблюдений,
– число наблюдений,
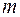 – число параметров при переменной
– число параметров при переменной 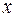 .
.
Фактическое значение 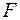 - критерия сравнивается с табличным при уровне значимости
- критерия сравнивается с табличным при уровне значимости 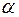 и числе степеней свободы
и числе степеней свободы 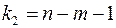 (для остаточной суммы квадратов) и
(для остаточной суммы квадратов) и 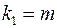 (для факторной суммы квадратов).
(для факторной суммы квадратов).
О качестве нелинейного уравнения регрессии можно судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по формуле
Пример 14.
Данные результатов наблюдений представлены в таблице 38.
Таблица 38 – Результаты наблюдений.
| X | -2 | -1 | |||
| У | 4,8 | 0,4 | -3,3 | -0,8 | 3,2 |
Определить методом наименьших квадратов параметры a0, a1, a2 зависимости вида 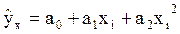
Решение методом Крамера.
Составим вспомогательную таблицу и произведем расчеты, необходимые для составления системы нормальных уравнений (таблица 39).
Таблица 39 – Расчетные показатели.
| № | X | У | X2 | X3 | X4 | X У | X2 У |
| -2 | 4,8 | -8 | -9,6 | 19,2 | |||
| -1 | 0,4 | -1 | -0,1 | 0,4 | |||
| -3,3 | |||||||
| -0,8 | -0,8 | -0,8 | |||||
| 3,2 | 6,4 | 12,8 | |||||
| сумма | 4,3 | -4,4 | 31,6 |
На основании полученных результатов расчета коэффициентов система нормальных уравнений примет вид
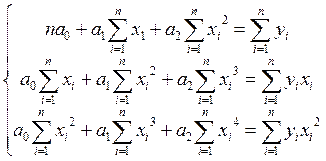 =
= 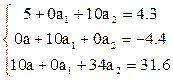
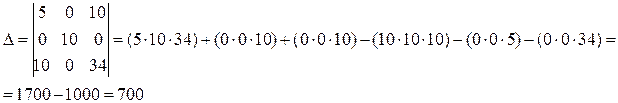
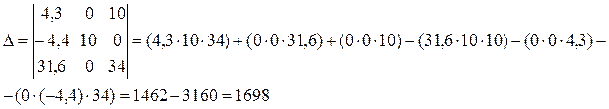
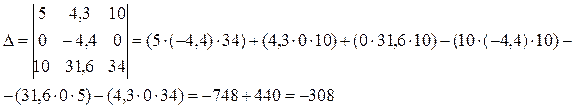
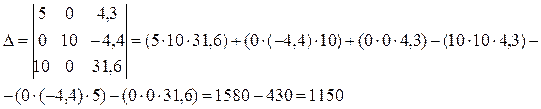

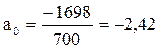 ,
, 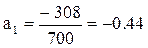 ,
, 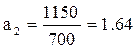
Таким образом, уравнение нелинейной регрессии на у примет вид
y = -2,42-0,44x+1,64х2.
Путем подстановки значений x, получаем расчетные значения y:
ŷ1= -2,42-0,44·(-2)+1,64· (-2)2=5,02
ŷ 2=-2,42-0,44·(-1)+1,64· (-1)2=-0,34 т.д.
Результаты вычислений оформляют в таблице 40 ст. 4
Рассчитываем среднее значение y
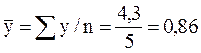
Рассчитываем значения в таблице 40.
Таблица 40 – Расчетные показатели.
| № | x | y |  | y-  | (y- 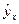 )2 )2 | (ˉ 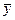 -y) -y) | (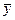 -y)2 -y)2 |
| 3 | |||||||
| -2 | 4,8 | 5.02 | -0.22 | 0.0484 | 3.94 | 15.5236 | |
| -1 | 0,4 | -0.34 | 0.74 | 0.5476 | -0.46 | 0.2116 | |
| -3,3 | -2.42 | -0.88 | 0.7744 | -4.16 | 17.3056 | ||
| -0,8 | -1.22 | 0.42 | 0.1764 | -1.66 | 2.7556 | ||
| 3,2 | 3.26 | -0.06 | 0.0036 | 2.34 | 5.4756 | ||
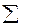 | 4,3 | - | - | 1.5504 | - | 41.272 |
Уравнение нелинейной регрессии, дополняем показателем корреляции, индексом корреляции R:
Вычисляем индекс корреляции по формуле
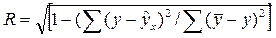 =
= 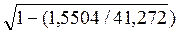 =0,981
=0,981
Индекс корреляции близок к единице, поэтому можно сделать вывод о довольно тесной связи между заданными величинами.
Текущий контроль знаний по теме:
1. Связь называется корреляционной:
а) если каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака;
б) если каждому значению факторного признака соответствует множество значений результативного признака, т.е. определенное статистическое распределение;
в) если каждому значению факторного признака соответствует целое распределение значений результативного признака;
г) если каждому значению факторного признака соответствует строго определенное значение факторного признака.
2. По аналитическому выражению различают связи:
а) обратные; б) линейные;
в) криволинейные; г) парные.
3. Регрессионный анализ заключается в определении:
а) аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения;
б) тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи);
в) статистической меры взаимодействия двух случайных переменных;
г) степени статистической связи между порядковыми переменными.
4. Под частной корреляцией понимается:
а) зависимость результативного признака и двух и более факторных признаков, включенных в исследование;
б) связь между двумя признаками (результативным и факторным или двумя факторными);
в) зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
г) зависимость между качественными признаками.
5. Какое значение не может принимать парный коэффициент корреляции:
а) -0,973; б) 0,005;
в) 1,111; г) 0,721?
6. При каком значении линейного коэффициента корреляции связь между признаками У и X можно считать тесной (сильной):
а) -0,975; б) 0,657;
в) -0,111; г) 0,421?
7. Какой критерий используют для оценки значимости коэффициента корреляции:
а) F-критерий Фишера;
в) критерий Пирсона;
г) δ-критерий Дарбина—Уотсона?
8. Если парный коэффициент корреляции между признаками У и X равен -1, то это означает:
а) отсутствие связи;
б) наличие обратной корреляционной связи;
в) наличие обратной функциональной связи;
г) наличие прямой функциональной связи?
9. Если парный коэффициент корреляции между признаками У и X принимает значение 0,675, то коэффициент детерминации равен:
а) 0,822; б) -0,675;
в) 0,576; г) 0,456?
10. Согласно методу наименьших квадратов минимизируется следующее выражение:
а) 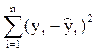 б)
б) 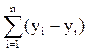 ;
;
в) 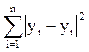 ; г)
; г) 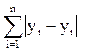 ?
?
11. Оценки параметров регрессии (свойства оценок МНК) должны быть:
а) несмещенными;
б) гетероскедатичными;
в) эффективными;
г) состоятельными?
12. В уравнении линейной парной регрессии параметр а1 означает:
а) усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов;
б) среднее изменение результативного признака при изменении факторного признака на 1%;
в) на какую величину в среднем изменится результативный признак у, если переменную х увеличить на единицу измерения;
г) какая доля вариации результативного признака у учтена в модели и обусловлена влиянием на нее переменной х?
13. Значение параметра а1 в уравнении линейной парной регрессии определяется по формуле:
а) 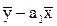 ; б)
; б) 
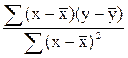 ;
;
в) 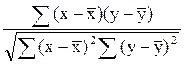 ; г)
; г) 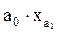 ?
?
14. Уравнение регрессии имеет вид ŷ = 2,02 ± 0,78х. На сколько единиц своего измерения в среднем изменится у при увеличении х ни одну единицу своего измерения:
а) увеличится на 2,02;
б) увеличится на 0,78;
в) увеличится на 2,80;
г) не изменится?
15. Какой критерий используют для оценки значимости уравнения регрессии:
а) F - критерий Фишера;
б) t - критерий Стьюдента;
в) критерий Пирсона;
г) d - критерий Дарбина - Уотсона?
16. Какой коэффициент определяет среднее изменение результативного признака при изменении факторного признака на 1%:
в) коэффициент корреляции;
17. Чему равен коэффициент эластичности, если уравнение регрессии имеет вид ŷ = 2,02 + 0,78x, если 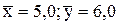 :
:
а) 0,94; б) 1,68;
в) 0,65; г) 2,42?
18. Уравнение степенной функции имеет вид:
а) 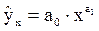 ; б)
; б) 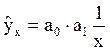 ;
;
в) 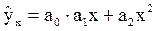 ; г)
; г) 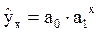 ?
?
19. Уравнение гиперболы имеет вид:
а) 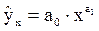 ; б)
; б) 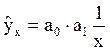 ;
;
в) 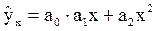 ; г)
; г) 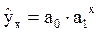 ?
?
Индекс корреляции определяется по формуле:
а) 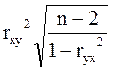 ; б)
; б) 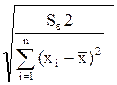 ;
;
в) 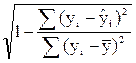 ; г)
; г) 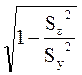 ?
?
 2015-05-18
2015-05-18 2831
2831