Способы устранения автокорреляции в модели множественной регрессии

Простой подход к учету коррелированности случайных членов регрессии 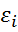заключается в предположении, что они образуют авторегрессионный процесс первого порядка

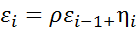(1)

Где 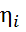~ N(0, 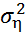), i=1,2,…,n, независимые случайные величины, а -коэффициент авторегрессии, 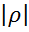<1. Случайный член в данном наблюдении связан лишь со случайным членом в предыдущем наблюдении. При 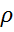>0 автокорреляция положительная, при 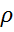<0-отрицательная, а при 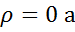втокорреляция отсутствует. В случае, когда коэффициент авторегрессии 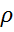известен, для исходного уравнения регрессии

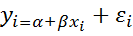(2)

можно выполнить авторегрессионное преобразование. Запишем это уравнение для предыдущего номера:

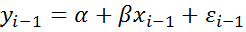, умножим его обе части на 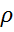и вычтем из предыдущего уравнения

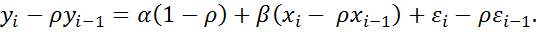(3)

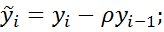
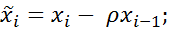
Если ввести новые переменные: 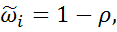то последнее уравнение можно записать в таком виде

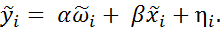(4)

В предположении, что для случайных членов первого уравнения справедливы условия Гаусса-Маркова, можно утверждать, что для модели (4) автокорреляция будет отсутствовать. Тогда метод наименьших квадратов позволяет для уравнения (4) определить оценки коэффициентов 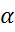, , 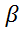которые будут несмещенными и эффективными оценками и для исходного уравнения (2). Однако, проблема заключается в том, что величина коэффициента авторегрессии 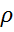неизвестна. Метод Кокрана-Оркатта представляет собой итеративный процесс определения параметров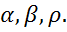

Шаг 1. Оценить регрессию y= 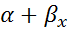+ 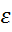в виде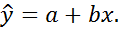

Шаг 2. Вычислить остатки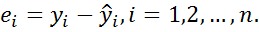

Шаг 3. Оценить регрессию вида 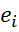= 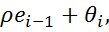где 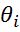-случайный член.

Шаг 4. Для оцененного значения найти оценки a,b коэффициентов 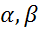соответственно преобразованного уравнения 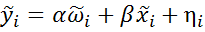,где =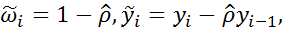

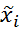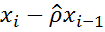
Шаг 5. Вернуться к шагу 2, если найденные оценки не совпадают с соответствующими оценками, полученными на предыдущей итерации, с заданной точностью.

Метод Халдрета –Лу использует перебор по значениям p из интервала (-1,1) с некоторым шагом при оценивании α, β по преобразованию уравнения (4). В процессе перебора определяется то значение р, при котором сумма кВ остатков для преобразования ур-я минимальна. Вблизи найденного минимума процедура может повторяться с более мелкими шагами до достижения заданной точности.