Посмотрим теперь, какие можно сделать теоретические заключения о форме 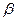 -спектра. Исследуем, каким образом энергия, выделяемая при b -распаде, распределяется между b -частицей и нейтрино.
-спектра. Исследуем, каким образом энергия, выделяемая при b -распаде, распределяется между b -частицей и нейтрино.
Какие факторы могут играть роль при b -распаде?
1) Кулоновское взаимодействие между конечным ядром и электроном. Им можно пренебречь только для самых легких ядер (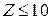 ) и достаточно больших энергий вылетающих электронов.
) и достаточно больших энергий вылетающих электронов.
2) Энергия отдачи ядра. Ею, практически, можно пренебречь всегда.
3) Масса нейтрино. Ею при рассмотрении формы можно пренебречь.
Вероятность 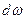 того, что при распаде электрон вылетит с импульсом в интервале
того, что при распаде электрон вылетит с импульсом в интервале 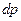 , а антинейтрино с импульсом в интервале
, а антинейтрино с импульсом в интервале 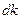 , очевидно, пропорциональна произведению этих дифференциалов. Но мы должны еще учесть закон сохранения энергии, согласно которому импульсы
, очевидно, пропорциональна произведению этих дифференциалов. Но мы должны еще учесть закон сохранения энергии, согласно которому импульсы 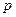 ,
, 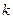 электрона и антинейтрино связаны соотношением
электрона и антинейтрино связаны соотношением
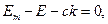
где кинетическая энергия электрона 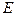 связана с его импульсом обычным релятивистским соотношением
связана с его импульсом обычным релятивистским соотношением
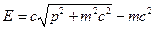 ,
,
а через 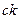 обозначена энергия антинейтрино с импульсом
обозначена энергия антинейтрино с импульсом 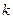 . (Такая связь энергии антинейтрино с его импульсом получится, если массу покоя этой частицы считать равной нулю.) Условие можно учесть введением в выражение для
. (Такая связь энергии антинейтрино с его импульсом получится, если массу покоя этой частицы считать равной нулю.) Условие можно учесть введением в выражение для 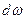
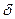 -функции
-функции
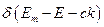 ,
,
по определению не равной нулю только при соблюдении.
Таким образом, вероятность 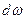 может быть записана в виде
может быть записана в виде
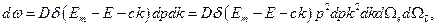
где 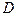 - некоторый коэффициент пропорциональности,
- некоторый коэффициент пропорциональности, 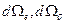 - элементы телесных углов направлений вылета электрона и антинейтрино. Вероятность
- элементы телесных углов направлений вылета электрона и антинейтрино. Вероятность 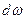 непосредственно связана с
непосредственно связана с 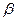 -спектром, поскольку для очень большого числа
-спектром, поскольку для очень большого числа 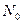 распадов число
распадов число 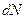 распадов с вылетом элетрона и антинейтрино с импульсом соответственно от
распадов с вылетом элетрона и антинейтрино с импульсом соответственно от 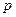 до
до 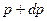 и от
и от 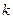 до
до 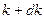 определяются соотношением
определяются соотношением
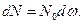
Коэффициент 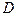 в, кроме мировых постоянных и константы, характеризующей интенсивность слабых взаимодействий, может еще зависеть от энергий
в, кроме мировых постоянных и константы, характеризующей интенсивность слабых взаимодействий, может еще зависеть от энергий 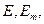 от взаимных ориентаций спинов и от угла между импульсами электрона и антинейтрино. Происхождение этих зависимостей может быть двояким. Во-первых, коэффициент
от взаимных ориентаций спинов и от угла между импульсами электрона и антинейтрино. Происхождение этих зависимостей может быть двояким. Во-первых, коэффициент 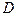 может зависеть от энергии за счет слабых взаимодействий. Такая зависимость будет проявляться во всех без исключения распадах, в том числе в распаде свободного нейтрона. Во-вторых, зависимость
может зависеть от энергии за счет слабых взаимодействий. Такая зависимость будет проявляться во всех без исключения распадах, в том числе в распаде свободного нейтрона. Во-вторых, зависимость 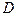 от
от 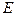 может возникнуть за счет особенностей структуры ядра. В этом случае
может возникнуть за счет особенностей структуры ядра. В этом случае 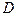 будет константой для распада свободного нейтрона и для тех распадов, при которых не меняется конфигурация нуклонов в ядре. В остальных случаях форма спектра будет различной для ядер разных типов.
будет константой для распада свободного нейтрона и для тех распадов, при которых не меняется конфигурация нуклонов в ядре. В остальных случаях форма спектра будет различной для ядер разных типов.
Рассмотрим сначала, какую форму будет иметь спектр при 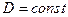 . В этом случае величину
. В этом случае величину 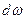 из можно проинтегрировать по всем углам и по абсолютному значению импульса нейтрино. Интегрирование по каждому телесному углу дает множитель
из можно проинтегрировать по всем углам и по абсолютному значению импульса нейтрино. Интегрирование по каждому телесному углу дает множитель 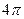 , а интегрирование по
, а интегрирование по 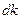 проводится с использованием основного свойства
проводится с использованием основного свойства 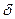 -функции (
-функции (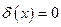 при
при 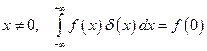 ). Поэтому при интегрировании по
). Поэтому при интегрировании по 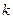
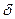 -функция исчезнет, а
-функция исчезнет, а 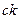 всюду измениться на
всюду измениться на 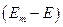 . После умножения на полное число распадов
. После умножения на полное число распадов 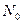 проинтегрированное выражение приобретает смысл числа электронов
проинтегрированное выражение приобретает смысл числа электронов 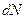 , вылетающих из ядра с импульсом, абсолютная величина которого лежит между
, вылетающих из ядра с импульсом, абсолютная величина которого лежит между 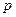 и
и 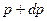 :
:
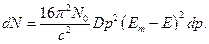
Чтобы получить распределение электронов не по импульсам, а по энергиям, надо в перейти от 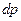 к
к 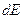
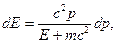
после чего выражающая форму 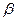 -спектра величина
-спектра величина 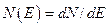 приобретает вид
приобретает вид
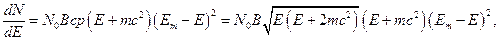
где 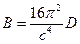 . В определенных случаях очень малых и очень больших энергий электрона формула несколько упрощается. Именно в нерелятивистском приближении
. В определенных случаях очень малых и очень больших энергий электрона формула несколько упрощается. Именно в нерелятивистском приближении
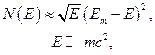
а в ультрарелятивистском случае
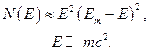
При малых энергиях вылетающей заряженной частицы форма 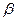 -спектра искажается под влиянием кулоновского взаимодействия между ядром и вылетающей из него заряженной частицей. При электронном распаде кулоновское взаимодействие является притягивающим, т. е. стремящимся уменьшить энергию вылетающего электрона. При позитронном распаде, напротив, кулоновское взаимодействие – отталкивающее так что оно ускоряет вылетающий позитрон.
-спектра искажается под влиянием кулоновского взаимодействия между ядром и вылетающей из него заряженной частицей. При электронном распаде кулоновское взаимодействие является притягивающим, т. е. стремящимся уменьшить энергию вылетающего электрона. При позитронном распаде, напротив, кулоновское взаимодействие – отталкивающее так что оно ускоряет вылетающий позитрон.
 2015-05-18
2015-05-18 676
676








