 | зависимых | ||
 | эндогенных | ||
| экзогенных | |||
| независимых |
Решение
Система эконометрических уравнений включает множество переменных, среди которых выделяют экзогенные и эндогенные переменные. В левой части системы эконометрических уравнений находятся только эндогенные (зависимые) переменные.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.
4. Установите соответствие между видом и классом системы эконометрических уравнений:
(1) 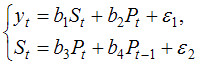
| система одновременных уравнений с лаговыми переменными | |||
| система независимых уравнений | |||
| система одновременных уравнений без лаговых переменных |
Решение
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части первого уравнения стоит переменная St, которая во втором уравнении находится в левой части, следовательно, система является системой одновременных уравнений. Во втором уравнении системы (1) одновременно с переменной Pt находится лаговая переменная Pt-1, поэтому система (1) является системой одновременных уравнений с лаговыми переменными.
В системе (2) в левой части представлены переменные yt и wt, которые не входят в правую часть уравнений системы, поэтому система (2) является системой независимых уравнений.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.
5. При построении систем эконометрических уравнений различают три класса моделей:
(1) система независимых уравнений;
(2) система рекурсивных уравнений;
(3) система одновременных уравнений.
Отнесите предложенные модели к соответствующему классу.
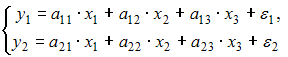 | |||
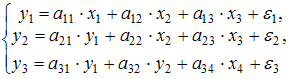 | |||
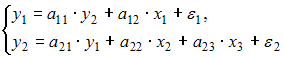 | |||
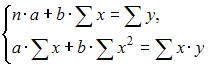 |
Решение
Модель, в которой 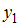 – продуктивность коров, можно назвать моделью экономической эффективности сельскохозяйственного производства. Эта модель содержит в правой части только независимые переменные, поэтому она может быть отнесена к классу «система независимых уравнений».
– продуктивность коров, можно назвать моделью экономической эффективности сельскохозяйственного производства. Эта модель содержит в правой части только независимые переменные, поэтому она может быть отнесена к классу «система независимых уравнений».
Модель, в которой 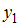 – производительность труда, может быть названа моделью производительности труда и фондоотдачи. Это модель содержит в первом уравнении только независимые переменные, а во втором уравнении в правой части встречается и зависимая переменная
– производительность труда, может быть названа моделью производительности труда и фондоотдачи. Это модель содержит в первом уравнении только независимые переменные, а во втором уравнении в правой части встречается и зависимая переменная 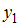 ; это значит, что модель можно отнести к классу «система рекурсивных уравнений».
; это значит, что модель можно отнести к классу «система рекурсивных уравнений».
Модель, в которой 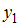 – темп изменения месячной заработной платы, может служить моделью динамики цены и заработной платы. В правых частях обоих уравнений содержатся зависимые переменные, поэтому данная модель может быть отнесена к классу «система одновременных уравнений».
– темп изменения месячной заработной платы, может служить моделью динамики цены и заработной платы. В правых частях обоих уравнений содержатся зависимые переменные, поэтому данная модель может быть отнесена к классу «система одновременных уравнений».
Система, в которой y – объем производства, вообще не является какой бы то ни было системой эконометрических уравнений – это система нормальных уравнений для определения параметров парной линейной регрессии.
Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
6. Модель равенства спроса и предложения, в которой предложение 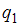 является линейной функцией цены p, а спрос
является линейной функцией цены p, а спрос 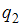 является линейной функцией цены p и дохода y, состоит из уравнений …
является линейной функцией цены p и дохода y, состоит из уравнений …
 | 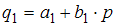 | ||
 | 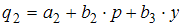 | ||
 | 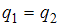 | ||
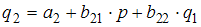 | |||
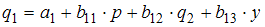 |
Решение
В модели предложение 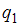 является линейной функцией цены p. Значит, уравнение для предложения
является линейной функцией цены p. Значит, уравнение для предложения 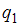 будет иметь вид
будет иметь вид 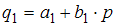 . Спрос
. Спрос 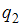 является линейной функцией цены p и дохода y, значит, уравнение для спроса
является линейной функцией цены p и дохода y, значит, уравнение для спроса 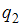 будет иметь вид
будет иметь вид 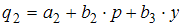 . Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим:
. Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим: 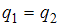 .
.
Модель будет иметь вид
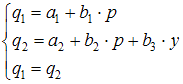
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 2015-05-18
2015-05-18 2125
2125
