Тема: Виды нелинейных уравнений регрессии. 1. Среди предложенных нелинейных зависимостей нелинейной по параметрам является

1. Среди предложенных нелинейных зависимостей нелинейной по параметрам является …

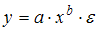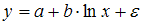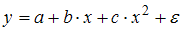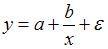Решение
Среди предложенных нелинейных зависимостей зависимость 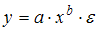является нелинейной по параметрам, но внутренне линейной, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции линейны по параметрам, но нелинейны относительно переменных и к линейному виду могут быть приведены с помощью замены переменных.

Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.

Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.

2. Гиперболической моделью не является регрессионная модель …

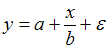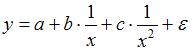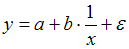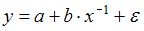Решение
Одним из видов нелинейных зависимостей в эконометрике являются гиперболические зависимости в виде функции, в которых независимая переменная находится в знаменателе дроби в степени (–1), (–2) и т.д. Как правило, в таких моделях параметры являются линейными. Рассмотрим уравнения:
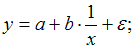
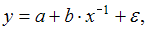которые представляют одну и ту же модель, так как 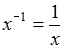и оба уравнения они отражают гиперболическую зависимость y от x.
В уравнении 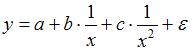независимая переменная x представлена в степени (–1) и (–2), и это тоже гиперболическая модель.
А в уравнении 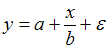переменная х представлена в степени 1, и это линейное уравнение регрессии с коэффициентом регрессии 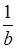. Поэтому уравнение 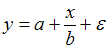не является гиперболической моделью.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 77.

3. Нелинейное уравнение парной регрессии вида 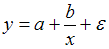является _____ моделью.

			гиперболической
			полиномиальной
			степенной
			показательной

Решение
Нелинейное уравнение парной регрессии вида 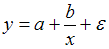является гиперболической моделью, так как теоретическое значение зависимой переменной 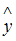рассчитывается в данном случае по формуле гиперболы .

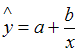Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 77.

4. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …

			степенной функции
			экспоненциальной функции
			параболы второй степени
			равносторонней гиперболы

Решение
Из перечисленных функций только степенная функция характеризуется постоянной эластичностью, следовательно, ее и нужно применить для отражения данной зависимости.

Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 89–92.

5. Степенной моделью не является регрессионная модель …

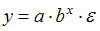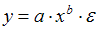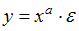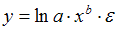Решение
Степенной моделью регрессии является такая модель, в которой независимая переменная х стоит в основании степени, а параметр – в показателе. Такими моделями из приведенных в ответах являются уравнения: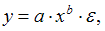
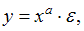
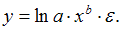
В уравнении 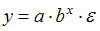независимая переменная х стоит в показателе степени, а параметр b – в основании, это не степенное уравнение, такая модель является примером показательной зависимости.

Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 77.