Аддитивную модель: Х=Т+S+E применяют в случае, когда амплитуда сезонных колебаний со временем не меняется. В противном случае используют мультипликативную модель: Х=Т × S × E.
Введем обозначения.
Пусть имеется временной ряд – Хij,
где i – номер сезона (периода времени внутри года, например месяца, квартала); i=1;L (L – число сезонов в году);
j – номер года, j=1;m (m – всего лет).
Тогда количество исходных уровней ряда равно
L × m=n.
Построение модели начинается с расчета сезонной компоненты. Только потом рассчитывают трендовую компоненту.
В качестве сезонной компоненты для аддитивной модели применяют абсолютное отклонение — Sai, для мультипликативной модели — индекс сезонности — Isi. Сезонные компоненты должны отвечать определенным требованиям:
• в случае аддитивной модели сумма всех сезонных компонент должна быть равна нулю;
• в случае мультипликативной модели произведение всех сезонных компонент должно быть равно единице.
Перед расчетом сезонных компонент ряд динамики выравнивают. Чаще всего используют механическое выравнивание (например, метод скользящей средней). В результате получают выровненный ряд: 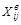 , который не содержит сезонной компоненты.
, который не содержит сезонной компоненты.
Абсолютное отклонение в 1-м сезоне определяется как среднее арифметическое из отклонений фактического и выровненного уровней ряда:
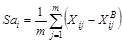
Индекс сезонности в i -м сезоне определяется как среднее арифметическое из отношений фактического уровня ряда к выровненному:
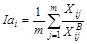 .
.
При построении трендовой компоненты модели временного ряда используют аналитическое выравнивание (см. п. 3.2). Данный метод выравнивания применяют не к фактическому ряду динамики, а к ряду, в котором исключена сезонная составляющая. Это означает, что исходные уровни ряда корректируются на величину сезонной компоненты. В случае аддитивной модели из исходных уровней вычитают Sai. В случае мультипликативной модели исходные уровни ряда делят на Isi.
Рассмотрим на примере построение аддитивной модели временного ряда. Пусть имеются поквартальные данные за 3 года об объемах выпуска продукции некоторым предприятием (в тыс. шт.). Данные приведены в табл. 3.4 (строки 1, 2,3).
Таблица 3.4
| Год | Квартал – i | Объем выпуска (Xtij) | 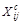 | 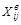 | 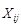 – – 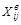 | 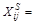 = = 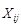 – – Sai – – Sai | T | 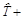 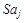 |
| 531,25 575,00 615,00 680,00 730,00 775,00 815,00 880,00 955,00 | 477,15 | 416,1 | 348,9 | |||||
| (1) | 401,60 | 474,8 | 473,2 | |||||
| 553,13 | 161,88 | 551,60 | 533Д | 696,8 | ||||
| 595,00 | 5,00 | 694,66 | 592,1 | 497,40 | ||||
| 647,50 | -62,50 | 652,15 | 650,8 | 583,6 | ||||
| (2) | 705,00 | -145,00 | 561,60 | 709,4 | 707,8 | |||
| 752,50 | 222,50 | 811,60 | 931,5 | |||||
| 795,00 | 5,0 | 894,66 | 826,7 | 732,1 | ||||
| 847,50 | -82,50 | 832,15 | 885,4 | 818,3 | ||||
| (3) | 917,50 | -197,50 | 721,60 | 944,1 | 942,5 | |||
| 1071,6 | 1002,7 | 1166,1 | ||||||
| 1194,6 | 1061,4 | 966,7 |
В нашем примере L = 4; m = 3; n = 12.
Для расчета сезонной компоненты проведем выравнивание уровней ряда методом скользящей средней. Период усреднения примем равным 4. Рассчитанная по 4-м уровням средняя 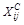 будет относиться к середине интервала усреднения (см. табл. 3.4, строка 4). Чтобы полученные средние привести в соответствие с фактическими моментами времени, найдем средние значения из двух последовательных скользящих средних - центрированные скользящие средние –
будет относиться к середине интервала усреднения (см. табл. 3.4, строка 4). Чтобы полученные средние привести в соответствие с фактическими моментами времени, найдем средние значения из двух последовательных скользящих средних - центрированные скользящие средние – 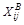 (табл. 3.4, строка 5).
(табл. 3.4, строка 5).
Для расчета абсолютных отклонений 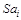 (i = 1; L) найдем разности между исходными –
(i = 1; L) найдем разности между исходными – 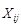 и выровненными –
и выровненными – 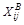 уровнями ряда (табл. 3.4, строка 6). Для дальнейшего расчета
уровнями ряда (табл. 3.4, строка 6). Для дальнейшего расчета 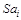 построим отдельную таблицу. Строки данной таблицы соответствуют сезонным компонентам, столбцы – годам. В теле таблицы находятся значения:
построим отдельную таблицу. Строки данной таблицы соответствуют сезонным компонентам, столбцы – годам. В теле таблицы находятся значения: 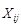 –
– 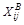 . По этим данным рассчитываются средние арифметические из абсолютных отклонений по каждой строке – (
. По этим данным рассчитываются средние арифметические из абсолютных отклонений по каждой строке – (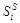 ).
).
Если сумма всех средних оценок равна нулю 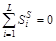 , то данные величины и будут окончательными значениями сезонных компонент (
, то данные величины и будут окончательными значениями сезонных компонент (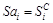 ). Если их сумма не равна нулю, то рассчитываются скорректированные значения сезонных компонент вычитанием из средней оценки величины, равной отношению суммы средних оценок сезонных компонент к их общему числу
). Если их сумма не равна нулю, то рассчитываются скорректированные значения сезонных компонент вычитанием из средней оценки величины, равной отношению суммы средних оценок сезонных компонент к их общему числу 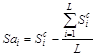 . Для нашего примера расчет значений
. Для нашего примера расчет значений 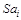 , представлен в табл. 3.5.
, представлен в табл. 3.5.
Таблица 3.5
| Номер компо-ненты | Год 1 | Год 2 | Год З | Средняя оценка сезонной компоненты 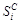 | Скорректиро-ванная сезонная компонента 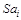 |
| – –1,67 123,33 –78,33 | –66,67 –5,00 180,00 –113,33 | –70,00 –1,67 183,33 – | –68,33 –2,78 162,22 –95,83 | –67,15 –1,60 163,40 –94,66 | |
| Итого | –4,72 |
Для определения трендовой компоненты устраним сезонные колебания из уровней исходного ряда: 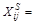
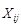 – Sai. Результаты расчета
– Sai. Результаты расчета 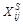 для нашего примера представлены в табл. 3.4, строка 7. Далее строим уравнение регрессии для уровней
для нашего примера представлены в табл. 3.4, строка 7. Далее строим уравнение регрессии для уровней 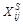 – уравнение тренда:
– уравнение тренда: 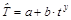 (где ty – условная переменная времени). Расчет параметров см. в п. 3.2. Окончательно имеем:
(где ty – условная переменная времени). Расчет параметров см. в п. 3.2. Окончательно имеем: 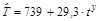 . Рассчитанные по уравнению тренда уровни ряда
. Рассчитанные по уравнению тренда уровни ряда 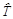 занесем в табл. 3.4 строка 8.
занесем в табл. 3.4 строка 8.
Теперь смоделируем уровни ряда в соответствии с аддитивной моделью, т. е. прибавим к 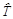 вычисленное ранее значение абсолютного отклонения –
вычисленное ранее значение абсолютного отклонения – 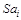 . Результаты занесем в последнюю строку табл. 3.4.
. Результаты занесем в последнюю строку табл. 3.4.
Результаты моделирования представлены на рис. 3.1.
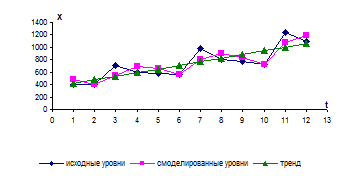
Рис. 3.1. Исходный ряд динамики и ряд, построенный по аддитивной модели
 2015-05-18
2015-05-18 5131
5131
