Проверка общего качества уравнения регрессии

Наиболее часто в практических расчетах для оценки качества всего уравнения в целом применяется коэффициент детерминации 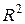, который рассчитывается по формуле

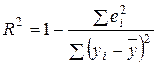, (2.2.2)

где 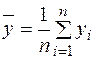. Коэффициент детерминации характеризует долю общего разброса значений зависимой переменной 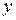, объясненного уравнением регрессии. Считается, что чем больше эта доля, тем лучше уравнение регрессии описывает исследуемую зависимость. В общем случае .

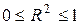Коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Это значит, что при добавлении новых объясняющих переменных значение коэффициента детерминации будет расти, хотя это и не обязательно означает улучшение качества регрессионной модели. Поэтому предпочтительнее использовать скорректированный коэффициент детерминации 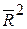, определяемый по формуле

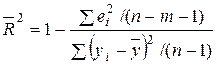. (2.2.3)

Соотношение (2.4.2) может быть представлено в следующем виде:

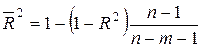. (2.2.4)

Обычно приводятся данные как по 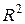, так и по 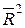. Доказано, что 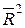увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t -статистика для этой переменной по модулю больше единицы.

Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о статистической значимости коэффициента детерминации:

, .

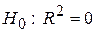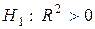Для проверки гипотезы используется следующая F- статистика:

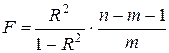. (2.2.5)

Проверка данной гипотезы равносильна проверке гипотезы о статистической незначимости уравнения регрессии:

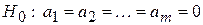
(все коэффициенты линейной регрессии, за исключением свободного члена, равны нулю). Ведь если коэффициенты равны нулю для генеральной совокупности, то уравнение регрессии должно иметь вид 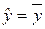, а коэффициент детерминации 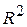и F -статистика Фишера также равны нулю. При этом их оценки для случайной выборки, конечно, отличаются от нуля.

Величина F при выполнении предпосылок МНК и при справедливости 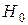имеет распределение Фишера. При заданном уровне значимости 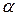по таблицам критических точек распределения Фишера находится критическое значение 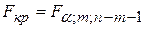. Если 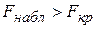, то основную гипотезу отвергают и принимают альтернативную гипотезу о статистической значимости уравнения регрессии. Если 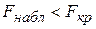, то основную гипотезу о незначимости уравнения регрессии не отвергают (уравнение модели признается незначимым).

Пример 2.2.3

Проверить качество оцененной модели (2.1.12) с помощью коэффициента детерминации.

Решение. Значение коэффициента детерминации рассчитаем по формуле (2.2.2):

.

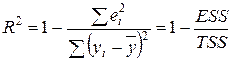Значение остаточной суммы квадратов отклонений вычислено в примере 2.1.2: ESS= 0,623. Вычисление TSS (общей суммы квадратов отклонений зависимой переменной от ее среднего выборочного значения) оформим в виде табл. 2.2.1.

Таблица 2.2.1

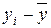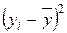	1,8	3,24
	-1,2	1,44
8,9	1,7	2,89
	1,8	3,24
7,1	-0,1	0,01
3,2	-4
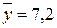	Сумма	26,28

Таким образом,

.

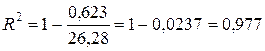Анализ статистической значимости коэффициента детерминации 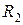осуществляется на основе F -статистики (2.2.5):

.

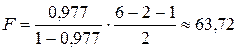Критическое значение для доверительной вероятности 0,95 равно 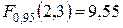. Так как 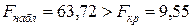, то коэффициент детерминации признается статистически значимым. Таким образом, построенное уравнение регрессии объясняет 97,7 % разброса зависимой переменной.

По формуле (2.2.4) скорректируем значение коэффициента детерминации с учетом числа факторных переменных:

,

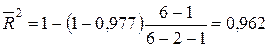что несколько меньше, чем обычный коэффициент детерминации.

Вопросы для самопроверки

1. В чем заключается нулевая гипотеза при проверке значимости коэффициентов регрессии?

2. Как проверяется значимость коэффициентов регрессии?

3. Как строятся интервальные оценки коэффициентов регрессии и в чем их суть?

4. В чем суть коэффициента детерминации ?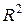

5. Чем скорректированный коэффициент детерминации отличается от обычного?

6. Как осуществляется анализ статистической значимости коэффициента детерминации?