После определения точечных оценок 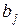 коэффициентов
коэффициентов 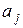 теоретического уравнения регрессии могут быть рассчитаны интервальные оценки коэффициентов. Если
теоретического уравнения регрессии могут быть рассчитаны интервальные оценки коэффициентов. Если 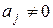 , то статистика
, то статистика 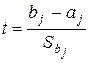 имеет распределение Стьюдента с
имеет распределение Стьюдента с 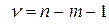 степенью свободы.
степенью свободы.
По таблице критических точек распределения Стьюдента по требуемому уровню значимости 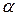 и числу степеней свободы
и числу степеней свободы 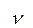 можно найти критическую точку
можно найти критическую точку 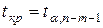 , удовлетворяющую условию
, удовлетворяющую условию
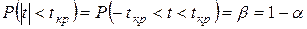 .
.
Подставив в это соотношение вместо 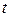 статистику
статистику 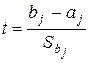 , после преобразований получим
, после преобразований получим
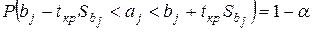 .
.
Таким образом, доверительный интервал, накрывающий с доверительной вероятностью 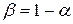 неизвестное значение параметра
неизвестное значение параметра 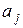 , определяется неравенством
, определяется неравенством
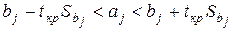 . (2.2.1)
. (2.2.1)
Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый коэффициент принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Пример 2.2.2
Построить доверительный интервал, который с доверительной вероятностью 0,95 накроет истинные значения параметров 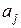 , j=0,1,2, модели (2.1.12).
, j=0,1,2, модели (2.1.12).
Решение. Критическое значение t- статистики равно 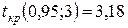 . По формуле (2.2.1) вычислим границы доверительных интервалов для параметров модели:
. По формуле (2.2.1) вычислим границы доверительных интервалов для параметров модели:
· для параметра 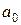 :
:
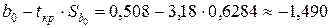 ,
,
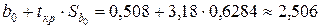 ,
,
· для параметра 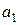 :
:
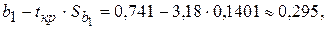
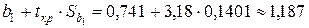 ,
,
· для параметра 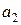 :
:
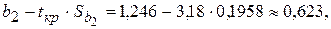
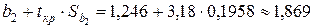 .
.
 2015-05-18
2015-05-18 1609
1609








