2015-05-18
557
Анализ статистической значимости коэффициента регрессии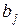 
осуществляется по схеме статистической проверки гипотез. Проверяют гипотезу 
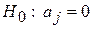(j -я независимая переменная не влияет на результат) при альтернативной гипотезе 
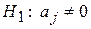(j -я независимая переменная влияет на результат).
Для проверки гипотезы используется t- статистика
,
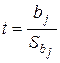которая при справедливости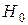 
имеет распределение Стьюдента с числом степеней свободы 
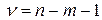. При требуемом уровне значимости 
наблюдаемое значение t -статистики сравнивается с критической точкой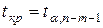 
распределения Стьюдента.
Если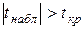 
, то коэффициент 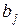считается статистически значимым,
т. е. гипотеза 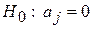отклоняется.
В противном случае (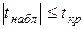
) коэффициент 
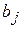считается статистически незначимым (статистически близким к нулю). Это означает, что фактор 
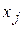линейно не связан с зависимой переменной 
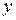. Поэтому после установления того факта, что коэффициент 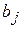статистически незначим, рекомендуется исключить из уравнения регрессии переменную .
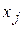Пример 2.2.1
Проверить статистическую значимость каждого коэффициента множественной регрессии (2.1.12).
Решение. Для проверки статистической значимости коэффициентов воспользуемся t -статистикой:
,
, 
, 
.
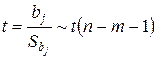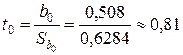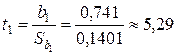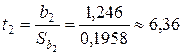Сравним вычисленные значения с критическим, выбранным из таблицы
t -распределения по числу степеней свободы n-m-1 =6-2-1=3 и уровню значимости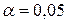 
, 
:
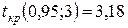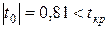– оценка параметра 
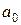статистически незначима;
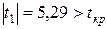– оценка параметра 
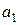статистически значима;
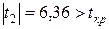– оценка параметра 
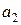статистически значима.
