Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Пусть дана идентифицируемая модель:
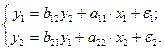 (4.5)
(4.5)
Если на параметр b 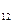 наложить ограничение, а именно
наложить ограничение, а именно 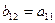 , то система превращается в простейшую сверхидентифицируемую модель
, то система превращается в простейшую сверхидентифицируемую модель
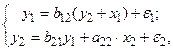 (4.6)
(4.6)
в которой 1-е уравнение уже является сверхидентифицируемым:
Н=1 (у 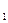 ), D=1 (х
), D=1 (х 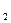 ), значит D+1>H.
), значит D+1>H.
Второе уравнение является (как и было) точно идентифицируемым:
Н=2 (у 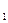 , у
, у 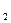 ), D=1 (х
), D=1 (х 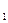 ), D+1=H.
), D+1=H.
Применим ДМНК к полученной модели (4.6):
1 шаг: применив МНК, найдем приведенную форму модели:
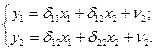
2 шаг: на основе 2-го уравнения данной системы, подставляя заданные значения х 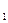 и х
и х 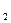 , определяем теоретические значения для эндогенной переменной у
, определяем теоретические значения для эндогенной переменной у 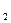 , т.е. у
, т.е. у 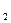 .
.
Введем новую переменную Z: Z= у 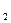 + х
+ х 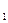 .
.
Тогда 1-е уравнение системы (4.6) 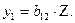
Применяя МНК к данному уравнению, находим 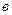
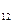 : S у
: S у 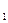 Z=
Z= 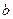
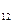 SZ
SZ 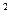 откуда
откуда 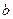
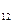 =S у
=S у 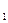 Z/SZ
Z/SZ 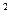 .
.
2-е уравнение системы (4.6) не изменилось, поэтому система одновременных уравнений будет иметь вид:
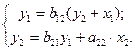
Приведем некоторые примеры применения эконометрических систем уравнений на практике.
К одной из распространенных систем одновременных уравнений относится статическая модель Кейнса, для описания народного хозяйства страны:
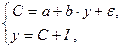
где С – личное потребление, у – национальный доход, I – инвестиции (все в постоянных ценах).
Другим примером может служить динамическая модель Кейнса:
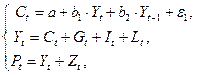
где У  , С
, С  , P
, P  - доход, частное потребление, ВНП, соответственно, в период времени t; У
- доход, частное потребление, ВНП, соответственно, в период времени t; У 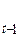 - доход предыдущего года; G
- доход предыдущего года; G  , I
, I  , L
, L  , Z
, Z  - соответственно, общественное потребление, валовые капиталовложения, изменения складских запасов, сальдо платежного баланса.
- соответственно, общественное потребление, валовые капиталовложения, изменения складских запасов, сальдо платежного баланса.
Большую популярность получила динамическая модель Клейна.
Система одновременных уравнений нашла применение в исследованиях спроса и предложения. Она имеет вид:
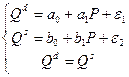
где Q 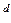 , Q
, Q 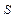 - объем спроса и объем предложения, Р - цена.
- объем спроса и объем предложения, Р - цена.
Построение системы структурных уравнений позволяет глубже изучить причины связи результирующих признаков. При этом происходит выделение и оценка косвенных и непосредственных влияний признаков.
 2015-05-18
2015-05-18 523
523








