2015-05-18
1909
Рассмотрим уравнение регрессии вида:
,
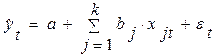где k – число независимых переменных модели.
Для каждого момента (периода) времени t =1: n значение компоненты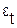 
определяется так: 
,
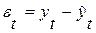или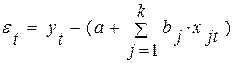 
.
При моделировании временных рядов нередко встречается ситуация, когда остатки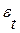 
содержат тенденцию (рис.5.2.б,в) или циклические колебания (рис.5.2.г), когда в соответствии с предпосылками МНК остатки 
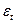должны быть случайными (рис. 5.2 а).
 |
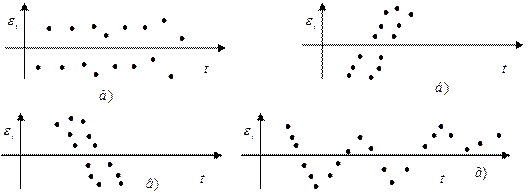Рис.5.2 Варианты изменения остатков временного ряда
В том случае, когда каждое следующее значение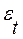 
зависит от 
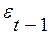, говорят о наличии автокорреляции остатков.
Причинами автокорреляции могут быть:
- исходные данные с ошибками в измерениях результативного признака;
- формулировка модели (модель может не включать фактор, оказывающий существенное воздействие на результат). Очень часто этим фактором является фактор времени t).
Если причина автокорреляции – в неправильной спецификации функциональной формы модели, то следует изменить форму связи факторных и результативных признаков.
Существуют два наиболее распространенных метода определения автокорреляции остатков: 1) путем построения графика зависимости остатков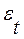 
от времени и визуальное определение наличия или отсутствия автокорреляции; 2) использование критерия Дарбина-Уотсона и расчет величины
.
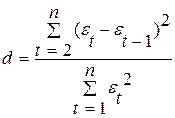Из данной формулы нетрудно вывести следующее соотношение между критерием Дарбина-Уотсона и коэффициентом автокорреляции остатков первого порядка
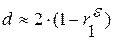, где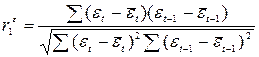 
Иными словами, если в остатках существует полная положительная автокорреляция и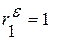 
, то d =0; если в остатках полная отрицательная автокорреляция 
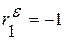, то, d =4; если автокорреляция остатков отсутствует, то 
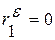и d =2.
Следовательно,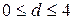 
.
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков. Альтернативные гипотезы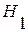 
и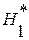 
состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона dL и dU для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости 
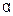. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1- 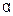) производится на основе данных, приведенных в таблице 5.1.
Механизм проверки гипотезы о наличии автокорреляции остатков. Таблица 5.1.
| Есть положительная автокорреляция остатков. Н0 отклоняется. С вероятностью Р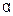=(1- ) принимается гипотеза Н1 | Зона неопределенности | Нет оснований отклонять Н0 (автокорреляция остатков отсутствует) | Зона неопределенности | Есть отрицательная автокорреляция остатков. Н0 отклоняется. С вероятностью Р=(1- 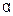) принимается гипотеза  |
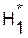| 0 dL dU 2 4-dU 4-dL 4 |
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу Н0.
Есть несколько существенных ограничений на применение критерия Дарбина – Уотсона:
- он непременим к модели авторегрессии;
- данный критерий можно использовать только для выявления автокорреляции остатков 1-го порядка;
- критерий дает достоверные результаты только для больших выборок.
