Задача 1. Измерить длину диагонали квадрата, считая, что единица длины есть сторона этого квадрата

Измерить длину диагонали квадрата, считая, что единица длины есть сторона этого квадрата.

Теорема Пифагора дает результат: искомая длина равна 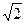. Предположение о том, что 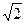= P/q – рациональное число опровергается известным доказательством от противного. Предположим, что 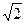= P/q Þ p 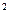= 2q 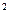Þ p=2k Þ 2q 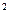= 4k 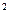Þ q = 2m Þ 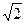= p/q.

Заметим, что величина 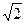является решением уравнения x 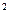-2=0. Действительные рациональные числа, являющиеся решениями алгебраических уравнений

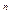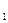x + a x 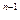+ … +a 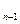x + a = 0 (10)

с целочисленными коэффициентами a 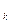Î Z, k=1, …, n, называются алгебраическими числами. Таким образом, число 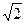является алгебраическим числом и является результатом алгебраической операции – извлечения корня.

Карл Фридрих Гаусс (1777 – 1855) доказал, см., например, [4], стр. 63, что алгебраические числа являются либо целыми числами, либо не представимы в виде p/q ни для каких целых p, q Î Z.